[백준] 최단거리 알고리즘 <2 : 벨만 - 포드>
0. 이전 글
이번 글에서는 다익스트라 알고리즘의 개념과 벨만 - 포드 알고리즘의 비교가 있을 예정이니 읽고 오면 좋다.
1. 벨만 - 포드 알고리즘의 소개
벨만 - 포드 알고리즘(Bellman-Ford Algorithm) 은 그래프에서 최단거리를 찾을 때 사용하는 알고리즘 중 하나이다. 특히 간선의 가중치가 음수가 되는 경우에도 사용할 수 있기 때문에 유용하다.
2. 다익스트라 vs 벨만 - 포드
그래프에서의 최단 거리 알고리즘을 사용한다면 역시 다익스트라 알고리즘과의 비교는 빼놓을 수 없다.
이전에 서술했듯이 다익스트라와 벨만 - 포드의 가장 큰 차이점은 음수인 간선이 존재하는 상태에서 풀 수 있느냐 없느냐로 나뉜다.
그림을 통해 다익스트라 알고리즘에서 음수인 간선이 있을 경우를 설명해보자.
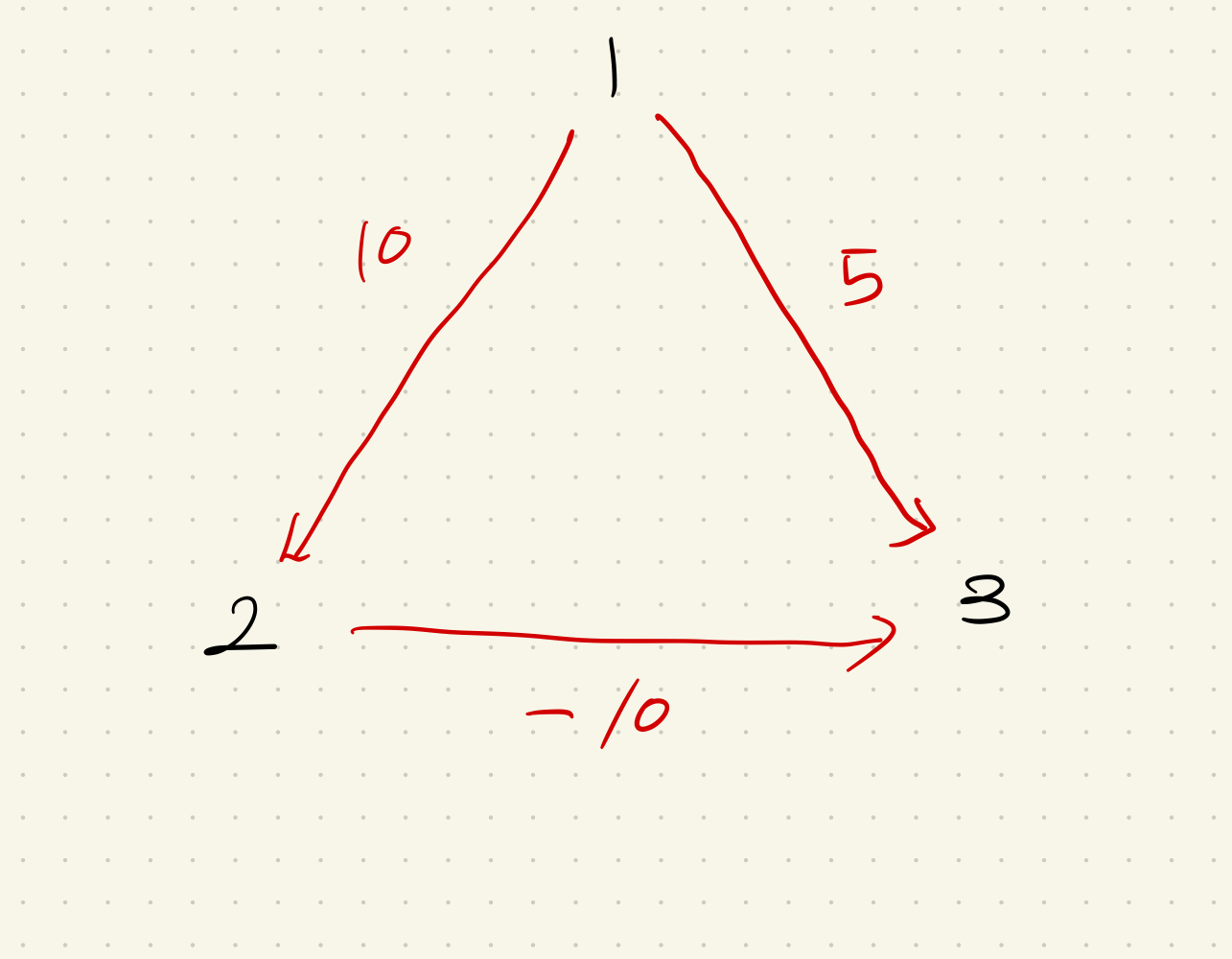
해당 그래프에서 1 노드 출발, 3 노드 도착의 경우 최소경로는
1 → 2 → 3 의 가중치 0의 경우이다.
하지만 이 그래프를 다익스트라 알고리즘으로 풀 경우 1에서 이동할 수 있는 2와 3의 경우에서 반드시 가중치가 작은 3을 선택하기 때문에 1 → 3 의 가중치 5의 경우로 끝나버린다.
벨만 - 포드 알고리즘의 경우 한 간선을 이동해 가중치를 계산할때마다 반복문을 통해 이동 가능한 모든 간선을 확인하기 때문에 다익스트라에 비해 시간은 오래 걸리지만 음수의 간선이 있을 경우도 확실하게 확인할 수 있다.
3. 벨만 - 포드 알고리즘 메커니즘
- 출발 노드를 설정한다.
- 최단거리 배열을 설정하고
inf값으로 초기화 한 후 출발 노드 값을 0으로 설정한다. - 모든 간선에 대해 확인하면서 각 노드로 갈 수 있는 최단 거리를 갱신해준다.
- 3의 과정을
(노드의 갯수 - 1)회 만큼 반복해준다. - 마지막 반복에서 최단거리가 갱신된다면 음의 순환이 있는 것으로 간주해 종료한다.
여기서 말하는 음의 순환이라는 것은 무엇일까? 그림으로 설명해보자.
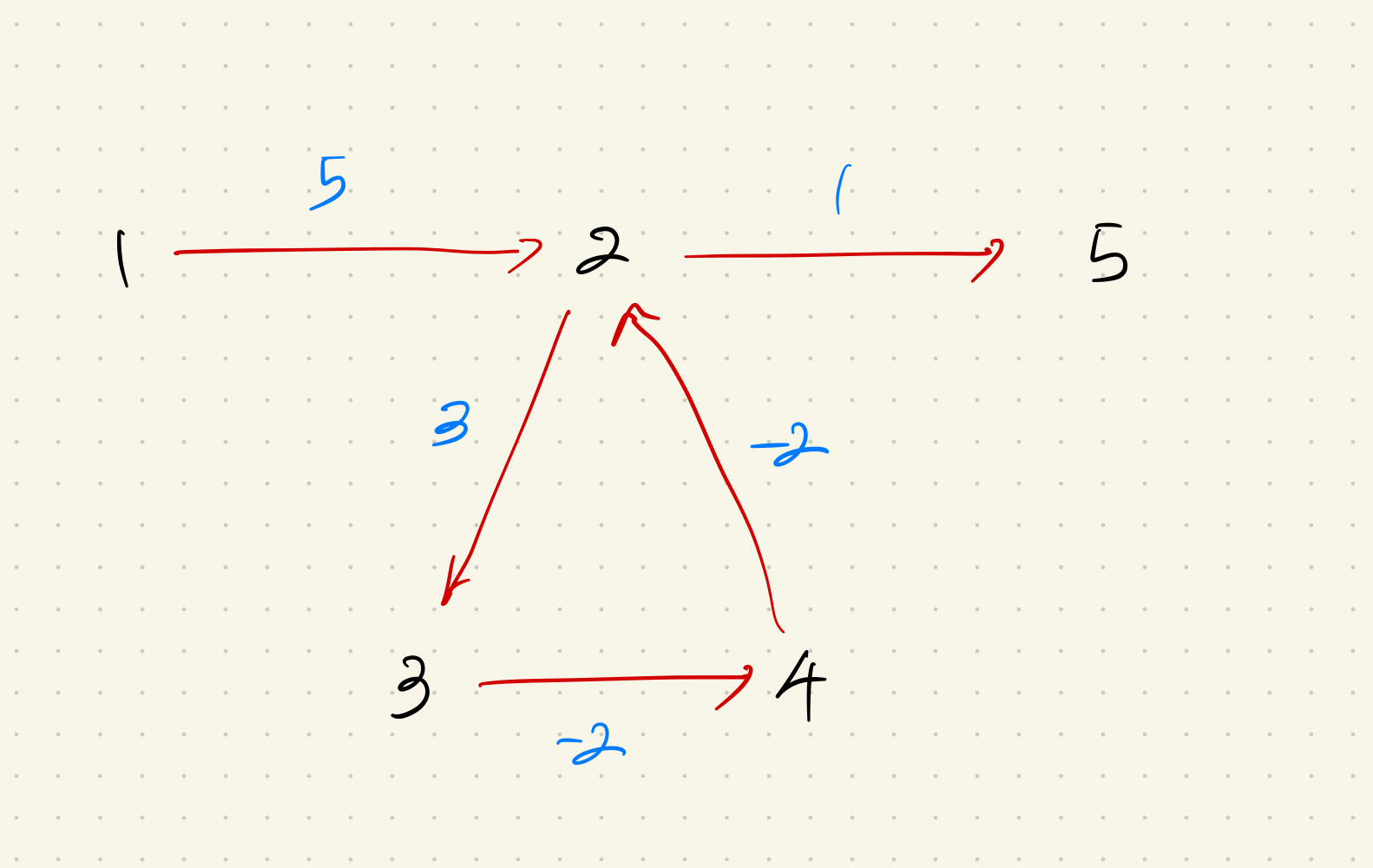
해당 그래프에서 1 에서 5로 간다고 해보자.
이때 2 → 3 → 4 를 순환하는 과정에서 총 가중치가 -1이 되도록 끊임없이 반복할 수 있기 때문에 5로 가는 전체 가중치가 -inf 값이 나온다.
그래프에선 아무리 많이 이동한다고 해도 최단 거리로 이동하기 위해선 최대 노드의 숫자-1 회 만큼 움직일 수 있다. 그렇기에 4의 과정에서 마지막 횟수에 최단거리 갱신이 일어난다면 그것은 음의 순환에 빠진 것이다.
그림의 예시로 벨만 - 포드 알고리즘의 작동 방식을 살펴보자.
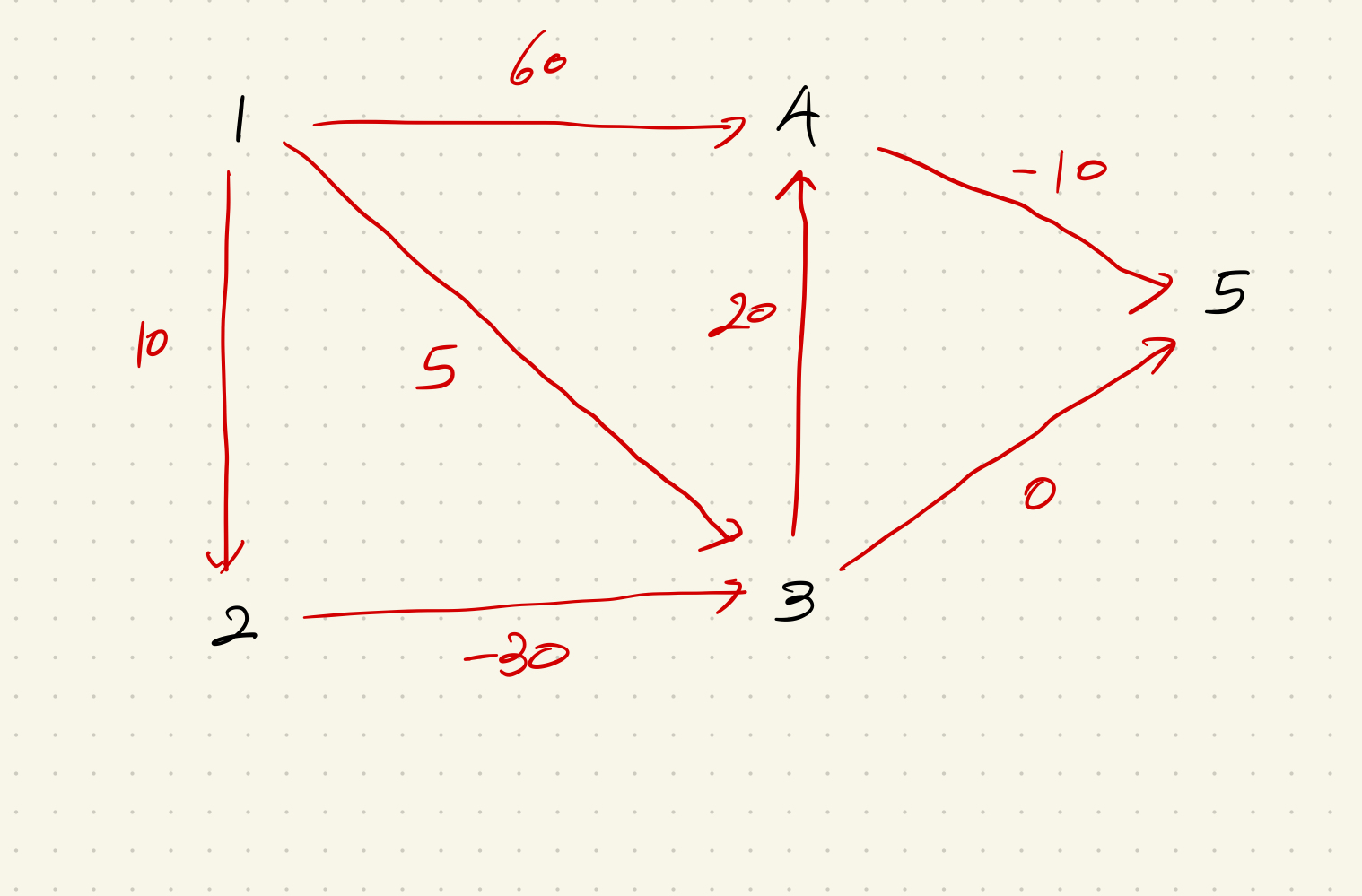
최단 경로 리스트를
inf로 초기화 한 후 출발지점을 0으로 설정한다. (이때 0은 더미 인덱스이다.)0 1 2 3 4 5 inf 0 inf inf inf inf 1에서 이동할 수 있는 모든 노드(2, 3, 4) 에 대한 거리를 계산 후 테이블에 적용한다.
0 1 2 3 4 5 inf 0 10 5 60 inf 다음번 이동 가능한 노드들에 대해서도 전부 확인한다. a. 1 → 2의 경우 10만큼 이동 후 2 → 3 으로 이동하는데 -30이 걸리므로 3은 -20이 된다. 이때 3의 최단경로는 5이기 때문에 -20이 더 작으므로 갱신 가능하다. b. 1 → 3의 경우 5의 가중치에 4 와 5로 이동 가능하므로 1 → 3 → 4의 경우 합 25, 1 → 3 → 5 의 경우 합 5 이다. 둘 다 현재 테이블의 최단경로보다 작으므로 갱신 가능하다. c. 1 → 4의 경우 현재 60의 가중치에 5로 이동하는 -10이 소모되어 50의 가중치로 이동 가능하다.
이때 a b c 중 무엇이 먼저 일어나든 항상 최소값만 선택하기 때문에 상관이 없다.
코드 상에서는 모든 노드에 대해서 확인하기 때문에 5번 노드 에서도 이동이 이루어진다. 하지만 5번 노드는 아직 inf 인 상태이기 때문에 5번 노드에서 이동할 수 있는 노드들은 갱신이 이루어지지 않는다. (inf가 inf 보다 작아지지 않으므로)
0 1 2 3 4 5 inf 0 10 -20 25 5 해당 과정을
노드의 갯수 - 1회 만큼 반복해준다.0 1 2 3 4 5 inf 0 10 -20 0 -20
4. 코드
기본적인 벨만 - 포드 알고리즘 사용을 테스트하는 문제이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
import sys
import math
read = sys.stdin.readline
node_count, edge_count = map(int,read().split())
graph = [[] for _ in range(node_count + 1)]
distance = [math.inf for _ in range(node_count + 1)]
infinit_cycle = False # 음의 순환을 감지하는 역할
for _ in range(edge_count):
u, v, w = map(int,read().split())
graph[u].append((v, w)) # 그래프의 인덱스에 해당 노드에서 이동 가능한 노드들을 입력
def bellman_ford(start):
global infinit_cycle
distance[start] = 0 # 출발 노드 0으로 초기화
for i in range(node_count): # 사이클 반복
for j in range(1,node_count+1): # 그래프 상의 모든 간선에 대해 확인한다.
for way in graph[j]:
desti = way[0]
weight = way[1]
if distance[desti] > distance[j] + weight: # 계산 결과가 기존 가중치보다 작은 경우
if i == node_count-1: # 마지막 cycle에서 갱신이 이루어지는 경우
infinit_cycle = True
break
distance[desti] = distance[j] + weight # 최단거리 그래프를 갱신
bellman_ford(1)
for answer in distance[2:]:
if infinit_cycle: # 음의 사이클이 있다면 -1 출력
print(-1)
break
else:
if answer > 1e9:
print(-1)
else:
print(answer)