[백준] DP <3>

0. 이전 글

DP <1>

DP <2>

DP를 사용한 다른 문제들은 해당 링크에 정리했다.

1. 냅색 알고리즘 소개.

냅색 알고리즘은 주어진 가방의 최대 중량 안에서, 물건들을 최대 가치만큼 넣었을 때의 최대 가치를 찾는 문제이다.

그림의 예를 들어보자.

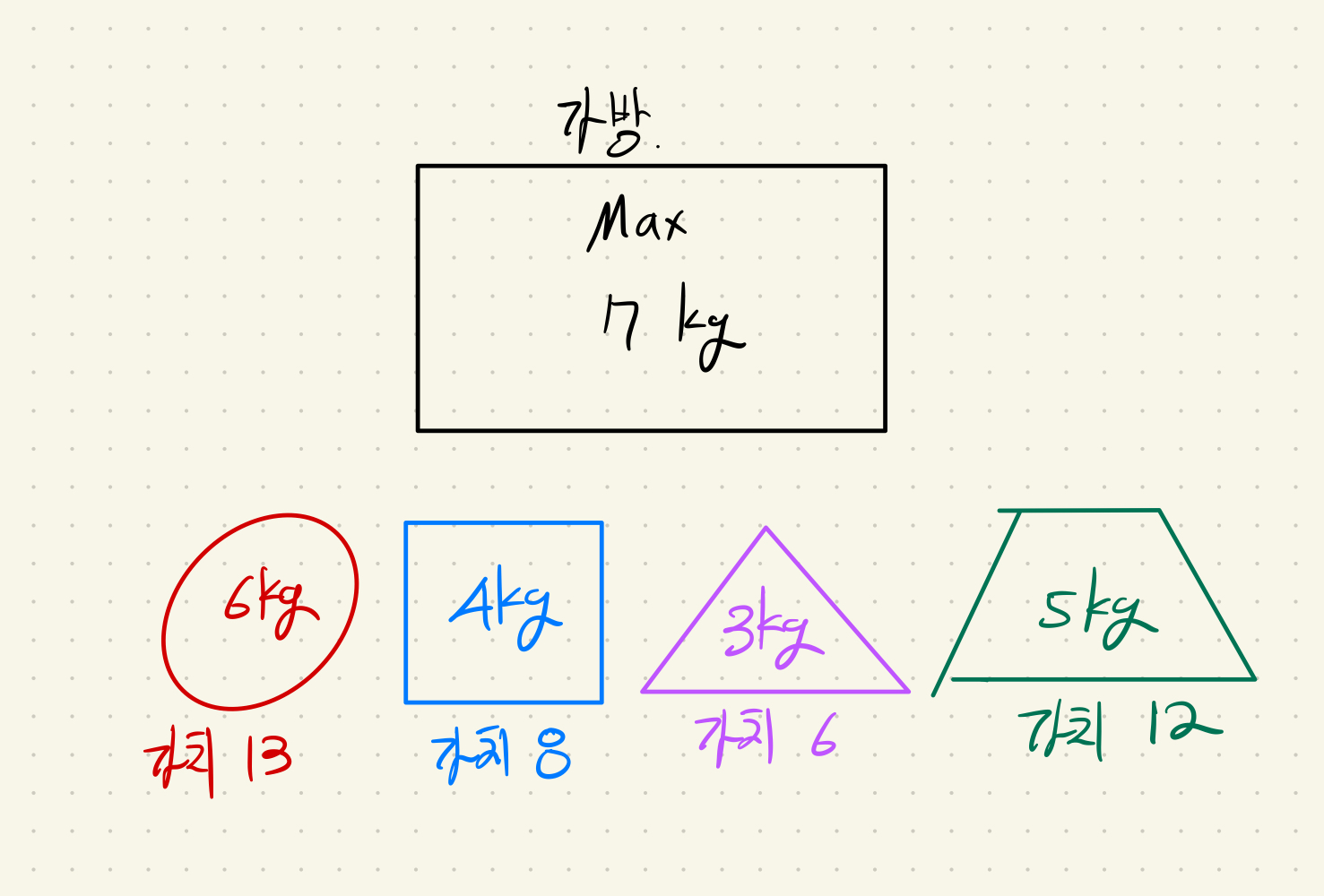
다음과 같은 예가 있다. 가방에 넣을 수 있는 최대 중량은 7kg이고, 물건은 4개가 있다.

이때 가방에 최대한 넣을 수 있으면서 가장 많은 가치를 담으려면 4kg 물건과 3kg 물건을 합쳐 가치 14를 담는 것이다. 사람의 눈으로 바로 보면 알 수 있지만 물건이 수십가지가 되는 경우엔 알기 어려울 것이다. 이 과정을 알고리즘으로 표현해야 한다.

2. 알고리즘 진행 방법.

물건이 주어졌을때, 기본적으로 가능한 행위는 2가지가 있다.

1. 현재 물건을 추가한다.
2. 현재 물건을 추가하지 않는다.

하지만 이 문제를 1차원 dp로 푼다면 불가능하다. 예를 들어 6kg의 물건이 먼저 들어오고, 뒤이어 4kg 물건과 3kg 물건이 온다면 후자의 두 물건을 넣는 것이 더 높은 가치를 가지지만, 6kg의 물건이 먼저 자리를 차지하고 있어 들어올 수 없기 때문이다. 즉 우리는 1번 행동에 추가 행동이 필요하다.

1. 현재 물건을 추가했을 경우, 남은 무게만큼의 최대 가치를 더한다.

우리는 물건이 들어있지 않은 과거의 상태까지 살펴보기 위해 2차원 table이 필요한 것이다. 2차원 table 이라면 이전 상태를 기록해놓고, 다시 사용이 가능하다.

해당 table엔 최대 중량이 N kg일 경우, 물건을 차례대로 살펴보면서 최대 가치를 기록한다.

최대 중량 \ 물건 종류	0번 물건(없음)	1번 물건(6kg, 13)	2번 물건(4kg, 8)	3번 물건(3kg, 6)	4번 물건(5kg, 12)
0	0	0	0	0	0
1	0	0	0	0	0
2	0	0	0	0	0
3	0	0	0	6	6
4	0	0	8
5
6
7

table의 i, j = 4, 3의 경우를 살펴보자.

이때 3번 물건을 추가하지 않는다면 가방엔 2번 물건만 들어있어 8의 가치이다.

3번 물건을 추가한다면 (현재 가방의 무게 - 지금의 무게) 가 최대중량인 상태에서 가장 현재 물건 전까지 살펴본 값에 현재 물건의 가치를 추가한다. 현재 가방의 무게는 4 이고, 지금의 무게는 3이니 i = 1이 된다. 그 상태에서 3번 물건 이전까지 살펴본 최대 가치는 0이다.(i = 1, j = 2) 즉 점화식으로 쓰자면 다음과 같다.

bags[i][j] = max(bags[i][j-1], bags[i - stuffs[j][0]][j-1] + stuffs[j][1])

i,j = 4,3 의 경우에

bags[i][j-1](물건을 추가하지 않은 경우) 는 8 이다.

bags[i - stuffs[j][0]][j-1] + stuffs[j][1] 은 6이다. (bags[1][2] + 3번물건 가치를 추가)

이 점화식대로 표를 채워가면 다음과 같아진다.

최대 중량 \ 물건 종류	0번 물건(없음)	1번 물건(6kg, 13)	2번 물건(4kg, 8)	3번 물건(3kg, 6)	4번 물건(5kg, 12)
0	0	0	0	0	0
1	0	0	0	0	0
2	0	0	0	0	0
3	0	0	0	6	6
4	0	0	8	8	8
5	0	0	8	8	12
6	0	13	13	13	13
7	0	13	13	14	14

즉 표를 완성시켰을 경우 가장 마지막행 마지막열이 답이 된다.

3. 코드

12865번 : 평범한 베낭

import sys

read = sys.stdin.readline

count, maxWeight = map(int,read().split())

stuffs = [[0,0]] # 0번 무게, 1번 가치

bags = [[0] * (count + 1) for _ in range(maxWeight + 1)]

for _ in range(count):
    stuff = list(map(int,read().split()))
    stuffs.append(stuff)

for i in range(1, maxWeight+1): # i = 최대중량
    for j in range(1, count+1): # j 물건
        if (stuffs[j][0] > i): # 현재 살펴보는 물건의 중량이 가방의 최대 중량보다 큰 경우
            bags[i][j] = bags[i][j-1]

        else: # 현재 살펴보는 물건의 중량이 최대 중량보다 작은 경우
        # 첫번째 -> 물건을 추가하지 않는다. #두번재 -> 현재 물건을 넣고, 남은 공간에 이전까지의 최대 가치를 찾아 넣는다
            bags[i][j] = max(bags[i][j-1], bags[i - stuffs[j][0]][j-1] + stuffs[j][1]) 

print(bags[-1][-1])