[백준] 최소 공통 조상
1. 최소 공통 조상 알고리즘 소개.
최소 공통 조상 (Lowest Common Ancestor)는 트리형 자료구조에서 임의의 두 노드가 갖는 가장 가까운 부모 노드를 찾는 알고리즘이다.
이때 트리의 형태는 이진 노드가 아니어도 상관없고, 전형적인 트리 구조라면 모두 가능하다. (즉 cycle이 있는 graph는 불가능하다.)
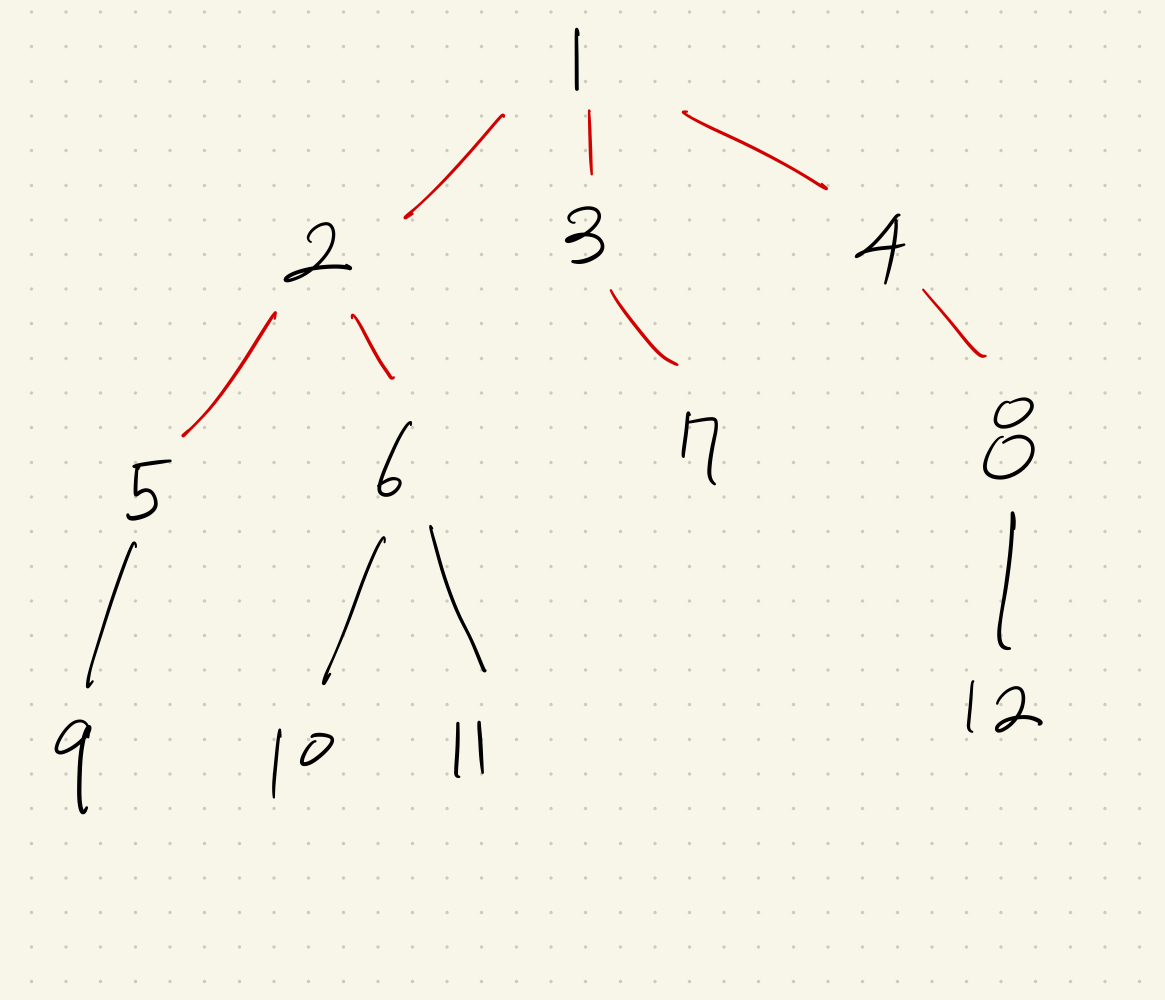
그림으로 예를 들어보자. 다음과 같은 트리가 있다고 했을 경우.
예시1) 9와 11의 공통노드
—> 2
예시2) 5와 3의 공통노드
—> 1
예시3) 4와 12의 공통노드
—> 4
즉 두 노드가 있을 때, 위 노드로 거슬러 올라가면서 만나는 최초의 노드를 찾는 과정이다. 이때 예시 3을 보면 자기 자신도 부모 노드의 일종으로 생각해야 한다.
2. LCA 알고리즘 진행.
LCA 알고리즘의 진행방식은 다음과 같다.
- 모든 노드에 대해 깊이를 계산.
- 공통 조상을 찾을 두 노드의 깊이가 같아지도록 한쪽 노드를 끌어올린다.
- 이후 부모가 같아질때까지 두 노드를 위쪽으로 한 칸씩 거슬러 올라간다.
진행 방식을 봤을 때, 우리에게 필요한 것은 다음과 같다.
- 모든 노드에 대한 깊이 데이터
a. 해당 계산을 수행할 dfs 함수 - 양방향 트리 그래프
- 부모 노드 데이터
- 공통 조상을 찾을 lca 함수
2.1 개선된 LCA
위에서 설명한 LCA은 최악의 경우 시간 복잡도가 O(N)이 소요된다.
해당 트리에서 9번 노드와 12번 노드의 공통 조상을 찾기 위해선 모든 노드를 거슬러 올라갸야 하기 때문이다.
하지만 약간의 트릭을 섞는다면 더 빠르게 거슬러 올라가는 방법이 있다. 바로 이분탐색을 활용하는 방법이다.
해당 블로그에서 자세히 설명해놓았다.
기존 LCA에선 1차원 부모 정보 배열을 두어 하나씩 거슬러 올라갔다. 개선된 LCA에선 2차원 부모 정보 배열을 만들어
Parent[x][k] = “x번 정점의 2^k” 번째 조상 노드의 번호” 를 저장한다.
2차원 부모 배열을 사용할 경우 기존에 선형적으로 탐색하는 방법에서 2의 제곱수만큼 뛰어넘으면서 탐색 가능하다.
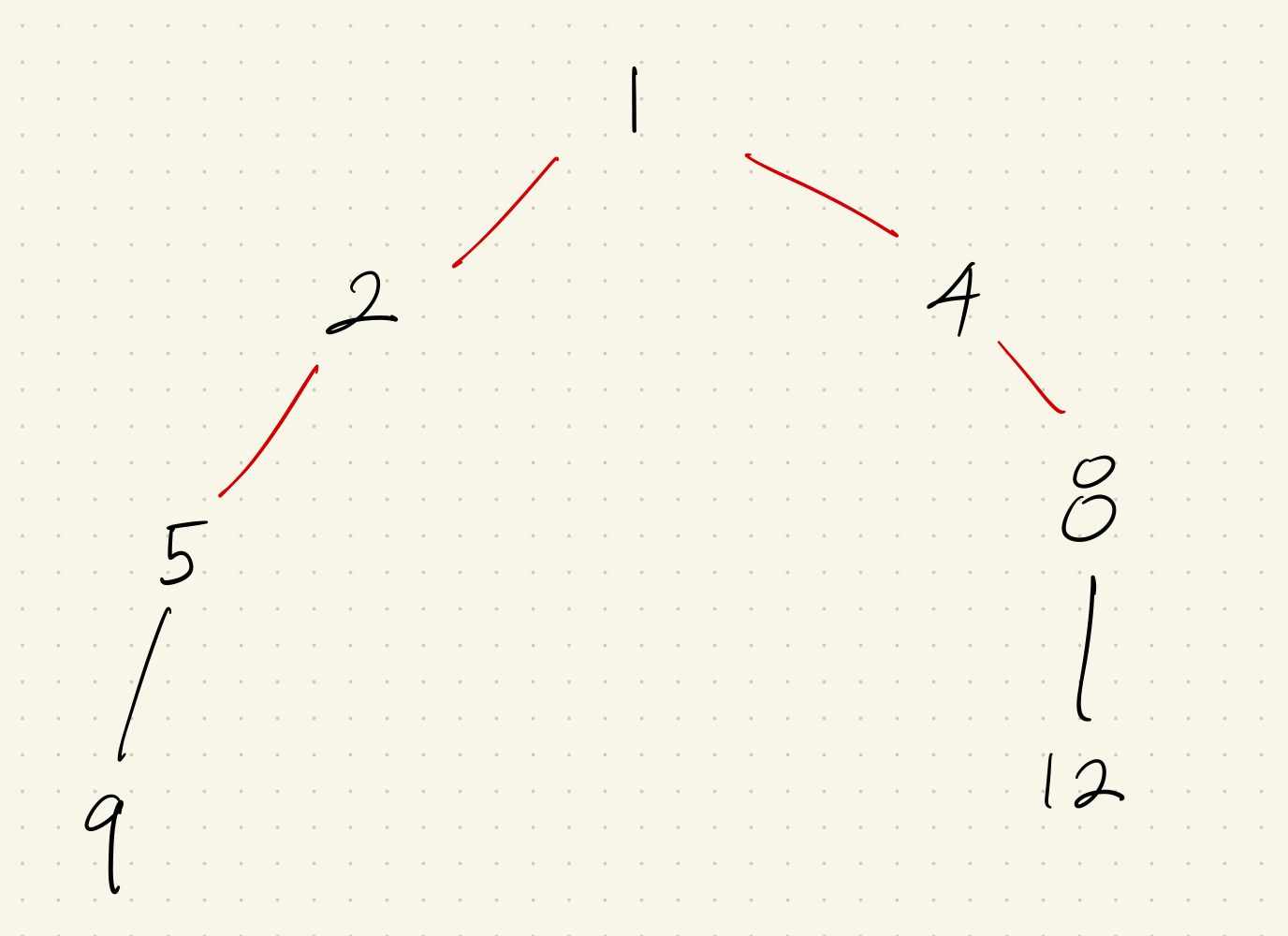
사진자리3
해당 그래프에서 13번과 4번의 공통 조상을 찾는다고 해보자. 두 노드의 깊이 차이는 3이다. 3을 이진수로 변환하면 “011” 이 되므로 우리는 2 만큼의 뛰어넘고 1만큼 뛰어넘어 2번으로 같은 레벨로 넘어갈 수 있다.(기존 방법으론 3번 이동해야 한다.)
3. 코드
3.1 기존 LCA 코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
import sys
sys.setrecursionlimit(int(1e5))
read = sys.stdin.readline
test_N = int(read())
def check_level(current, visited, depth): # 레벨 및 부모 정보 체크
visited[current] = True
level[current] = depth
for next_node in tree[current]:
if visited[next_node]: # 이미 방문했다면 패스
continue
parents[next_node] = current
check_level(next_node, visited, depth + 1)
def lca(a ,b): # 공통 조상 찾기
# 동일 깊이 맞춰주기
while level[a] != level[b]:
if level[a] > level[b]:
a = parents[a]
else:
b = parents[b]
# 동일 노드 맞춰주기
while a != b:
a = parents[a]
b = parents[b]
return a
for _ in range(test_N):
node_N = int(read())
visited = [0] * (node_N + 1) # 방문 했는지 안했는지 체크
level = [0] * (node_N + 1) # 깊이 정보 체크
parents = [0] * (node_N + 1) # 부모 체크
tree = [[] for _ in range(node_N + 1)]
target_node = []
for i in range(node_N):
parent, kid = map(int,read().split())
if i != node_N-1:
tree[parent].append(kid)
tree[kid].append(parent)
if i == 0:
root = parent
else:
target_node = [parent, kid]
check_level(root, visited, 0)
answer = lca(target_node[0], target_node[1])
print(answer)
3.2 개선된 LCA 코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
import sys
sys.setrecursionlimit(10**5)
read = sys.stdin.readline
N = int(read())
parent = [[0] * 21 for _ in range(N+1)]
graph = [[] for _ in range(N+1)]
visited = [False] * (N+1)
depth = [0] * (N+1)
for _ in range(N-1):
a, b = map(int,read().split())
graph[a].append(b)
graph[b].append(a)
def dfs(current, level): # dfs로 부모 찾기
visited[current] = True
depth[current] = level
for next_node in graph[current]:
if not visited[next_node]:
parent[next_node][0] = current
dfs(next_node, level + 1)
def lca(node1, node2):
# depth[node2] >= depth[node1]이 되도록 swap
if depth[node1] > depth[node2]:
node1, node2 = node2, node1
# 가장 깊은 경우부터 찾아준다.
for i in range(20, -1, -1):
if depth[node2] - depth[node1] >= (1 << i): # 두 노드의 거리
node2 = parent[node2][i]
# 같은 높이가 됐을 경우 두 노드의 값이 같으면 노드 값 하나 리턴하고 종료
if node1 == node2:
return node1
# 같은 높이가 됐을 경우 두 노드의 값이 다르면 올라가면서 공통 조상 찾기
else:
for i in range(20, -1, -1):
if parent[node1][i] != parent[node2][i]:
node1 = parent[node1][i]
node2 = parent[node2][i]
return parent[node1][0]
dfs(1,0)
for i in range(1, 21):
for j in range(1, N+1):
# 각 노드에 대해 2^i 번째 부모 정보 갱신
parent[j][i] = parent[parent[j][i-1]][i-1]
M = int(read())
for _ in range(M):
node1, node2 = map(int,read().split())
print(lca(node1, node2))