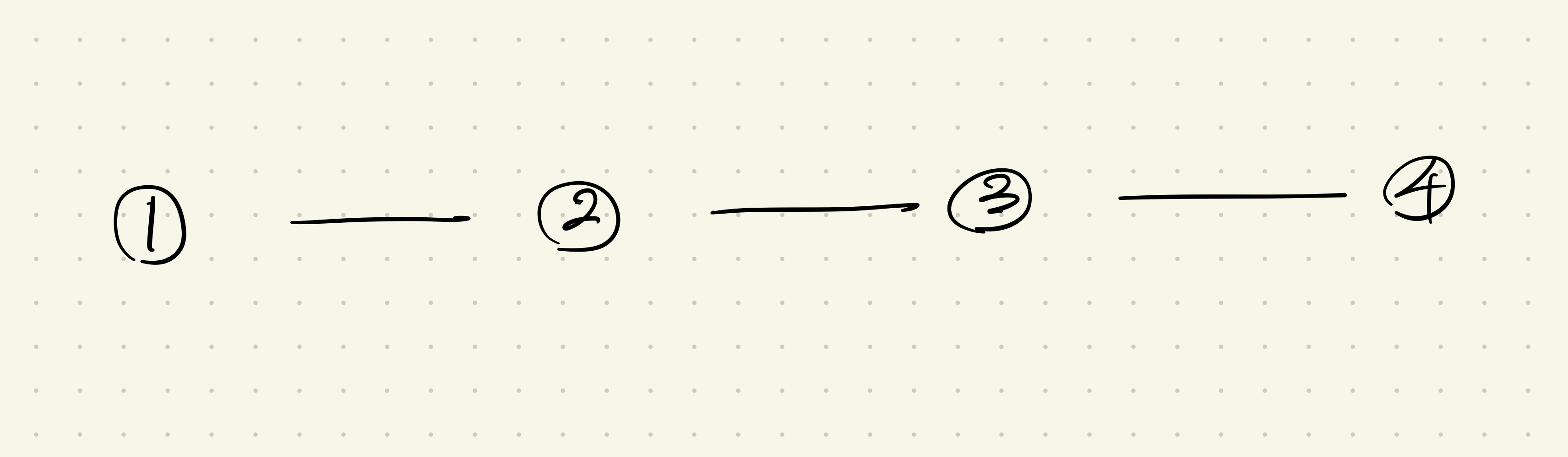[백준] 이분그래프

1. 이분 그래프의 정의

이분 그래프란 하나의 정점에서 나온 노드가 2개 이하이며, 2개인 경우 두 노드가 각각 인접하지 않도록 분할 가능한 경우를 뜻한다.

1.1 이분 그래프의 예

단순히 생각했을때 순환이 없는 경우만 거르면 될 것 같지만 약간 다르다.

일직선의 그래프의 경우 이분 그래프의 정의를 만족한다.

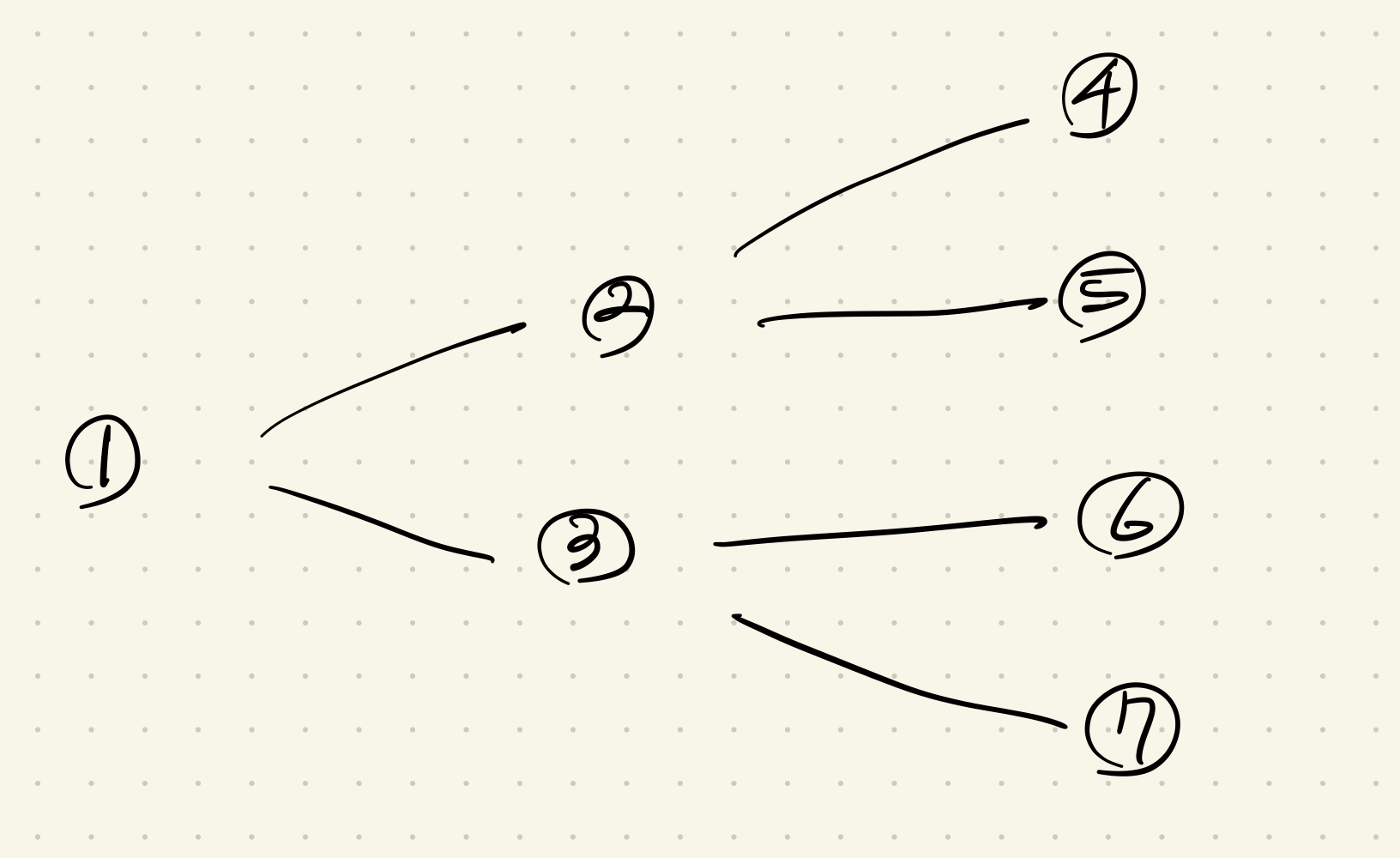
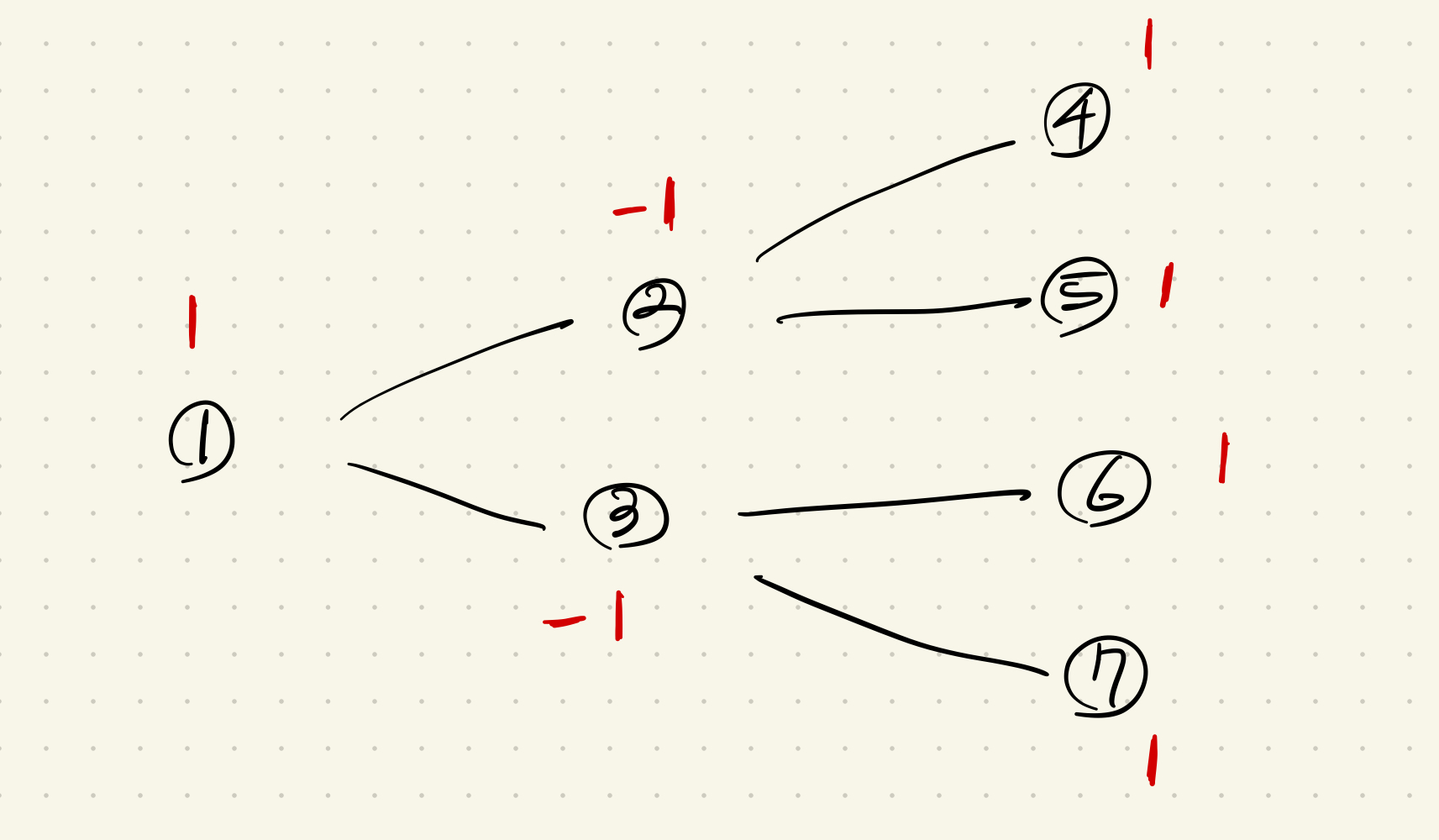
평범한 이진 트리의 경우도 이분 그래프의 정의를 만족한다.

(주의! 이진 트리와 이분 그래프는 다른 개념이다.)

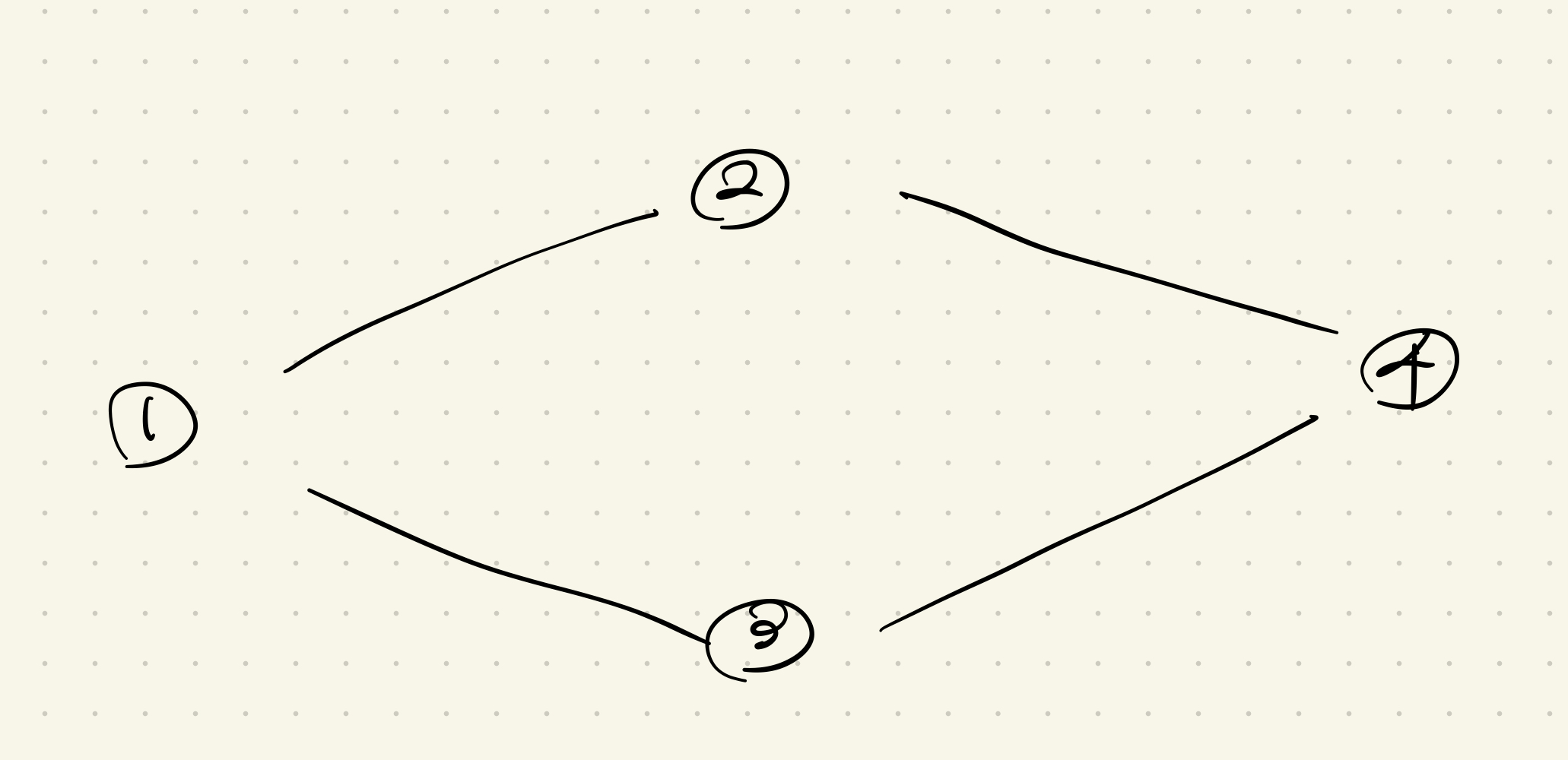
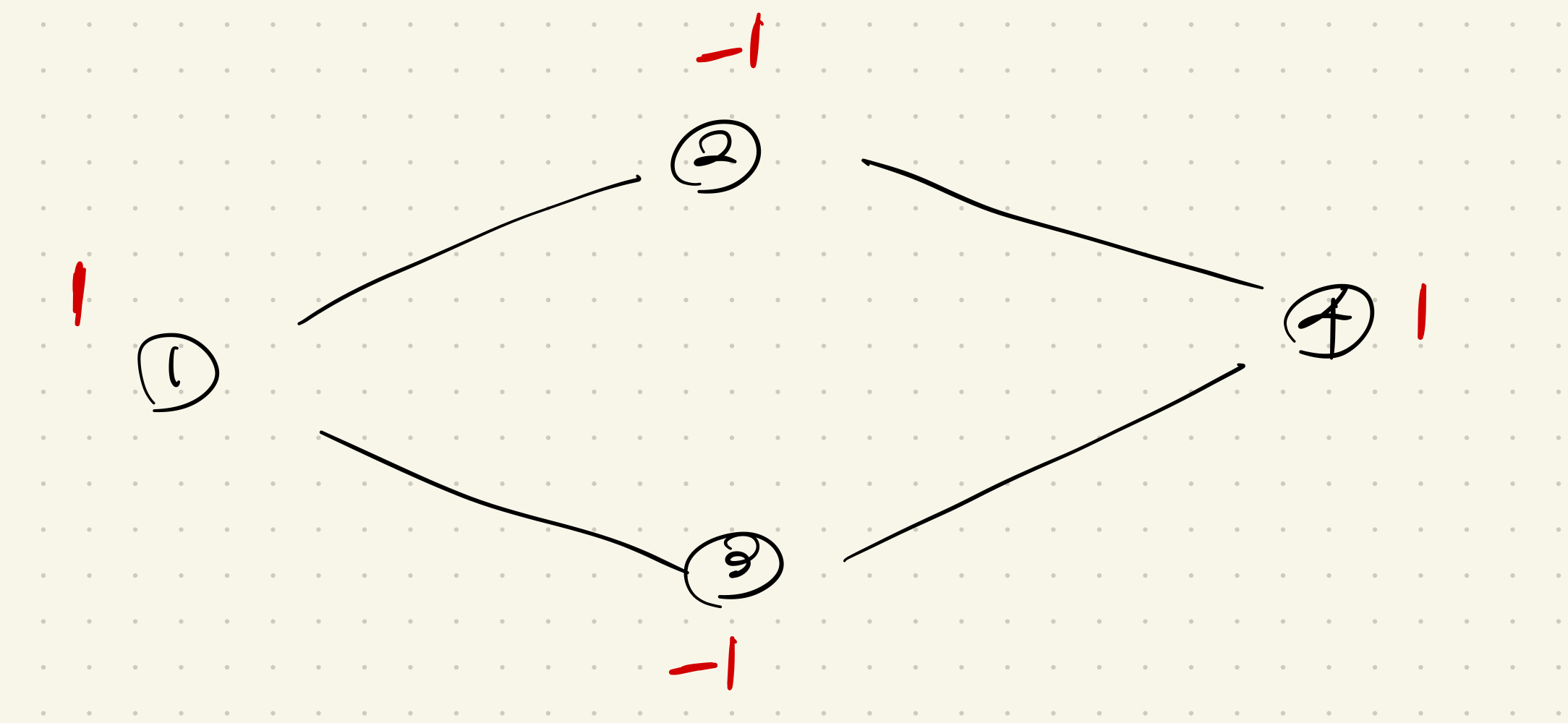
마름모꼴의 그래프도 이분 그래프의 정의를 만족한다.

이유는 한 가지 정점에서 나온 2와 3번 노드가 서로 인접하지 않기 때문이다.

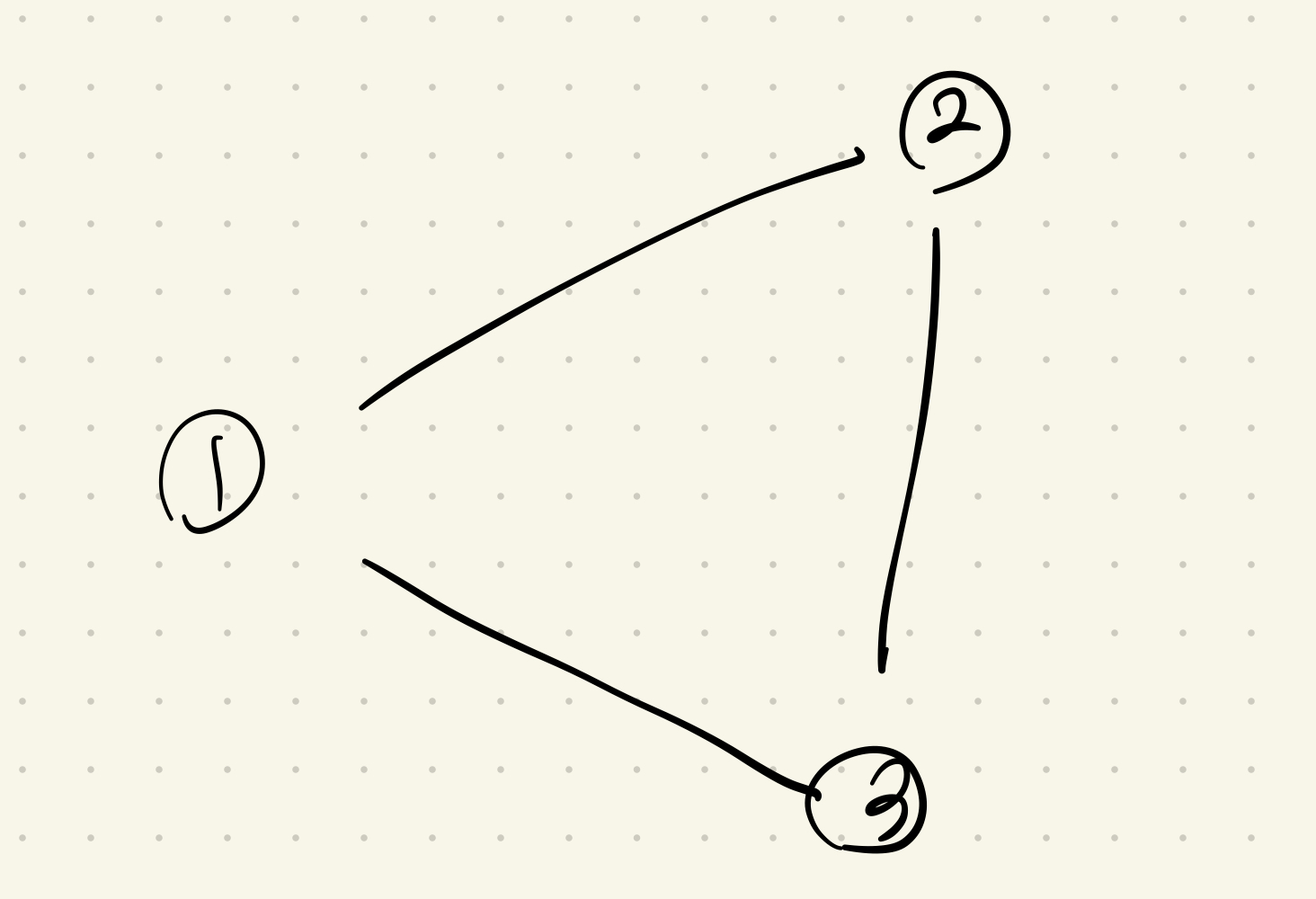
즉 불가능한 경우는 단 한가지이다.

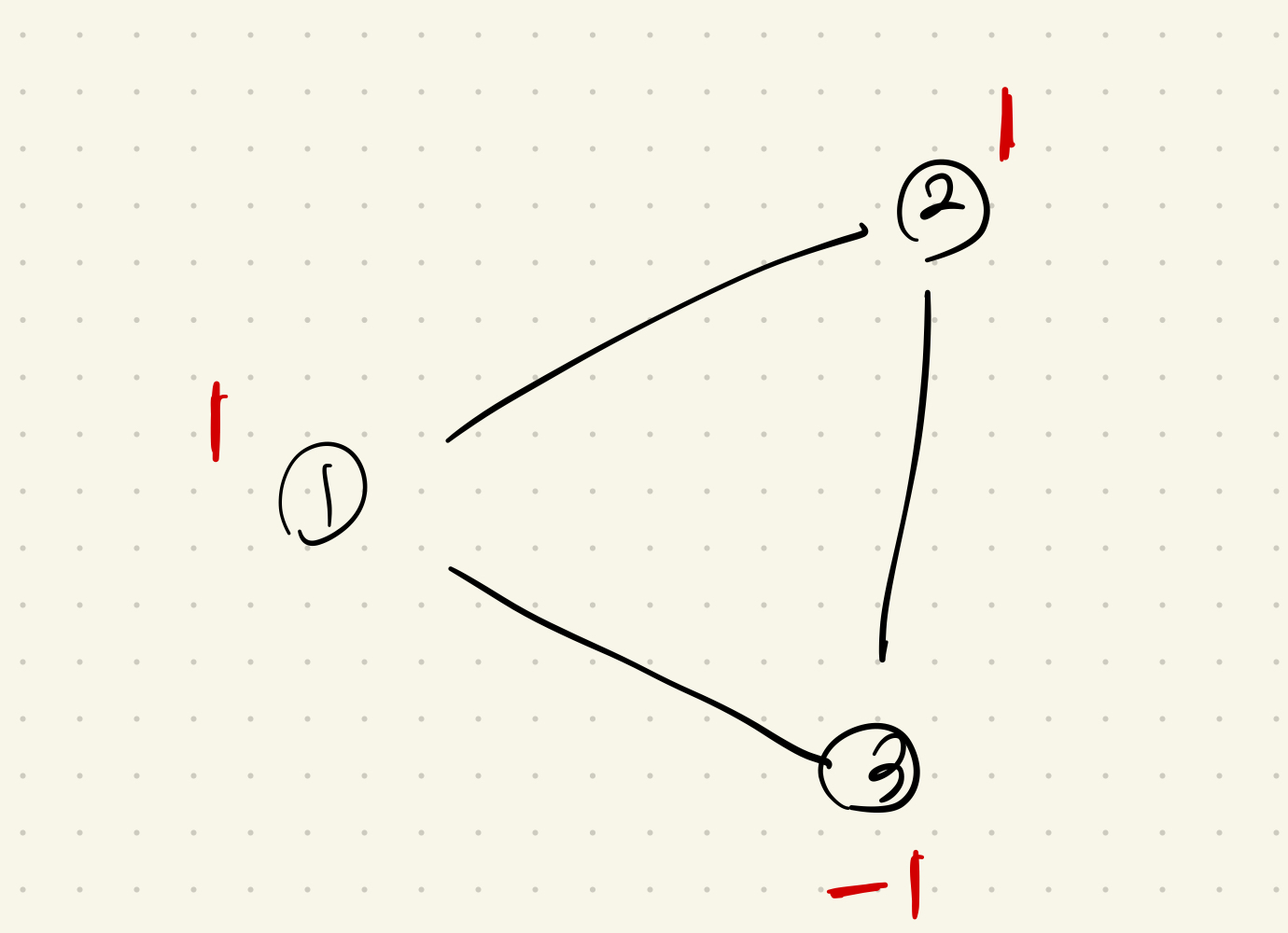
삼각형의 사이클을 이루고 있는 경우엔 불가능하다.

즉 이 문제는 그래프 상에서 단순히 사이클을 찾는 문제가 아니라 인접하고 있는 사이클을 찾아야 하는 문제이다.

2. 알고리즘 설명

나는 이번 문제에서 DFS를 활용한 무향 그래프 사이클 분별법을 사용했다.

평범한 DFS에서 몇 가지를 추가해주면 된다.

1. 이전 노드의 상태를 저장할 group 추가
2. DFS 순회 도중 이미 방문한 노드를 방문했을 경우 group을 비교
3. 만약 두 group이 같다면 사이클이 존재함.

이런 과정을 거쳐주는 이유는, DFS가 알고리즘 전개 상 반드시 방문했던 노드를 재방문 해야하는 과정이 있기 때문이다.

이때 방문했던 노드를 비교 시, 이전 노드와 group이 같다면, (즉 삼각형 사이클이 있는 경우) 사이클이 존재한다고 판단한다. 그림으로 확인해보자.

평범한 이진 트리 그래프라면 다음과 같은 group들을 갖는다.

마름모꼴 사이클 그래프라면 다음과 같은 group을 갖는다.

삼각형 사이클 그래프라면 다음과 같은 group을 갖는다.

즉 인접한 노드들끼리 같은 노드를 갖게 하면 안된다.

3. 코드

1707번 : 이분 그래프

import sys
sys.setrecursionlimit(10**5)
read = sys.stdin.readline

N = int(read())

# visited
# 0 == 방문하지 않음

def dfs(visited, current, graph, group):
    visited[current] = group
    nexts = graph[current]

    for next_go in nexts:
        if visited[next_go] == 0:
            if dfs(visited, next_go, graph, -group):
                return True
        else:
            if visited[next_go] == group:
                return True
            
    return False

def is_cycle(visited, graph):
    for node in range(1, len(graph)):
        if visited[node] == 0:
		        # 초기 group을 1로 설정
            if dfs(visited, node, graph, 1):
                return True
    return False

for _ in range(N):
    V, E = map(int,read().split())
    graph = [[] for _ in range(V+1)]
    visited = [0] * (V+1)

    for _ in range(E):
        u, v = map(int,read().split())
        graph[u].append(v)
        graph[v].append(u)
    
    if not is_cycle(visited, graph):
        print('YES')
    else:
        print('NO')