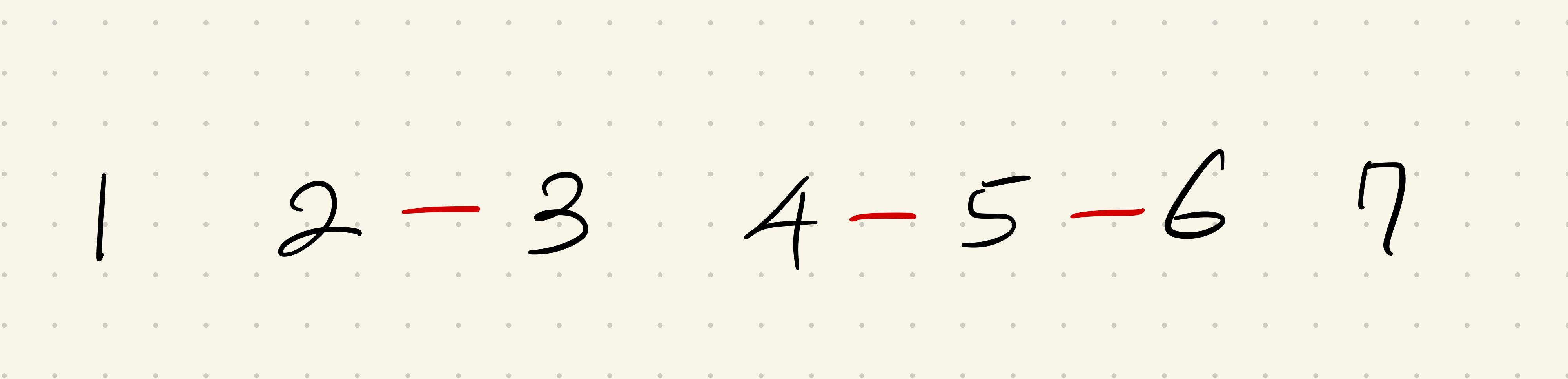[백준] 유니온 파인드

1. 유니온 파인드 알고리즘이란?

• 유니온 파인드란 그래프 자료구조에서 특정한 두 노드가 같은 그래프(같은 부모를 공유하는지)에 속하는지 알아보는 알고리즘이다.
• 두 노드를 합치는 Union, 두 노드가 같은 그래프에 속하는지 찾는 Find, 두 가지 부분으로 이루어진다.

2. 유니온 파인드의 예시

다음과 같은 그림에서 생각해보자.

노드 1, 2, 3, 4, 5, 6, 7이 존재한다.

이때 2와 3을 이어주고, 4와 5, 5와 6을 이어준다.

이때 임의의 노드 두 개를 골라 두 노드가 같은 집합에 속하는지 알아보아야 한다.

2 와 3은 같은 노드에 속한다.

4와 5, 4와 6, 5와 6은 같은 노드에 속한다.

1과 3, 1과 6, 5와 7은 다른 노드에 속한다.

이 알고리즘을 어떻게 구성해야 할까?

3. 유니온 파인드 알고리즘 진행.

1. 유니온 파인드 리스트를 준비한 후, 각각의 인덱스 번호로 초기화 시켜준다.

   이때 각각의 인덱스 번호로 초기화 하는 이유는, 자기 자신은 자신 넘버의 부모가 되기 때문이다.

   0	1	2	3	4	5	6	7
   0	1	2	3	4	5	6	7

2. 두 노드가 다른 집합에 속할 경우 합쳐준다(Union)

   예를 들어 2 와 3을 이어준다고 해보자.

   0	1	2	3	4	5	6	7
   0	1	2	2	4	5	6	7

   uf[3] = 2 로 변경해준다. 즉 uf[x] 의 값은 어느 부모를 가지고 있는지 알려준다.

   4와 5, 5와 6에 대해서도 같은 방식을 진행해준다.

   0	1	2	3	4	5	6	7
   0	1	2	2	4	4	5	7

3. uf table을 바탕으로 두 노드가 주어졌을 시, 같은 집합에 속하는지 아닌지 판단 가능하다.

3.1 알고리즘의 한계

해당 알고리즘을 자세히 생각해보면 비효율이 있다는 것을 알 수 있다.

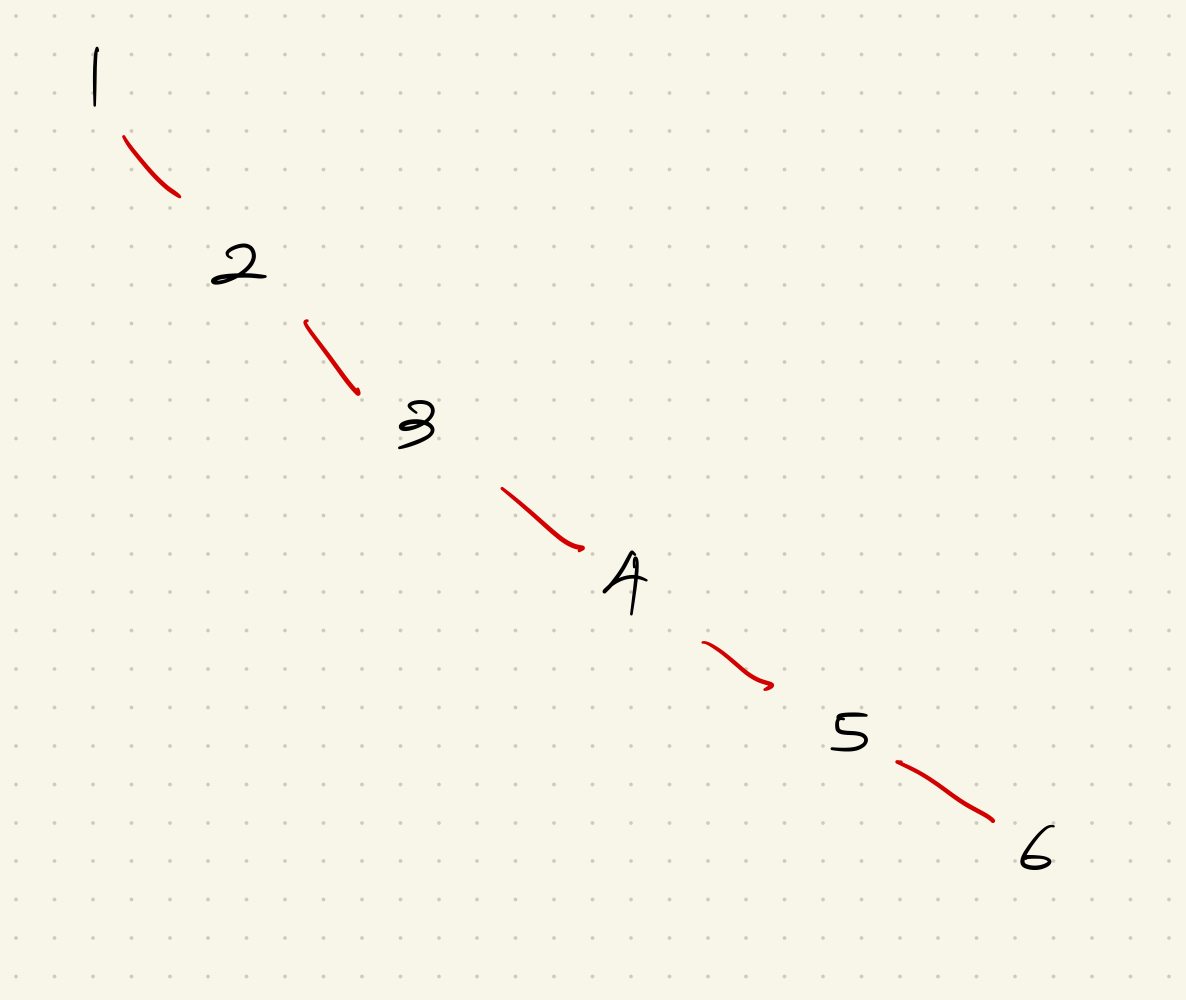
만약 그래프가 다음과 같이 구성되어 있다고 해보자.

이때의 uf table은 다음과 같이 구성될 것이다.

0	1	2	3	4	5	6
0	1	1	2	3	4	5

이때 1과 6이 같은 그래프에 속하는지 판단하려면 노드 6은 가장 부모인 1의 노드까지 재귀를 통해 계속 거슬러 올라가야 한다.

이런 일직선 그래프의 가장 비효율적인 경우를 해결하기 위해 한 가지 트릭이 필요하다.

3.2 알고리즘 개선

(본인 사견입니다. 정제된 설명은 다른 블로그로…)

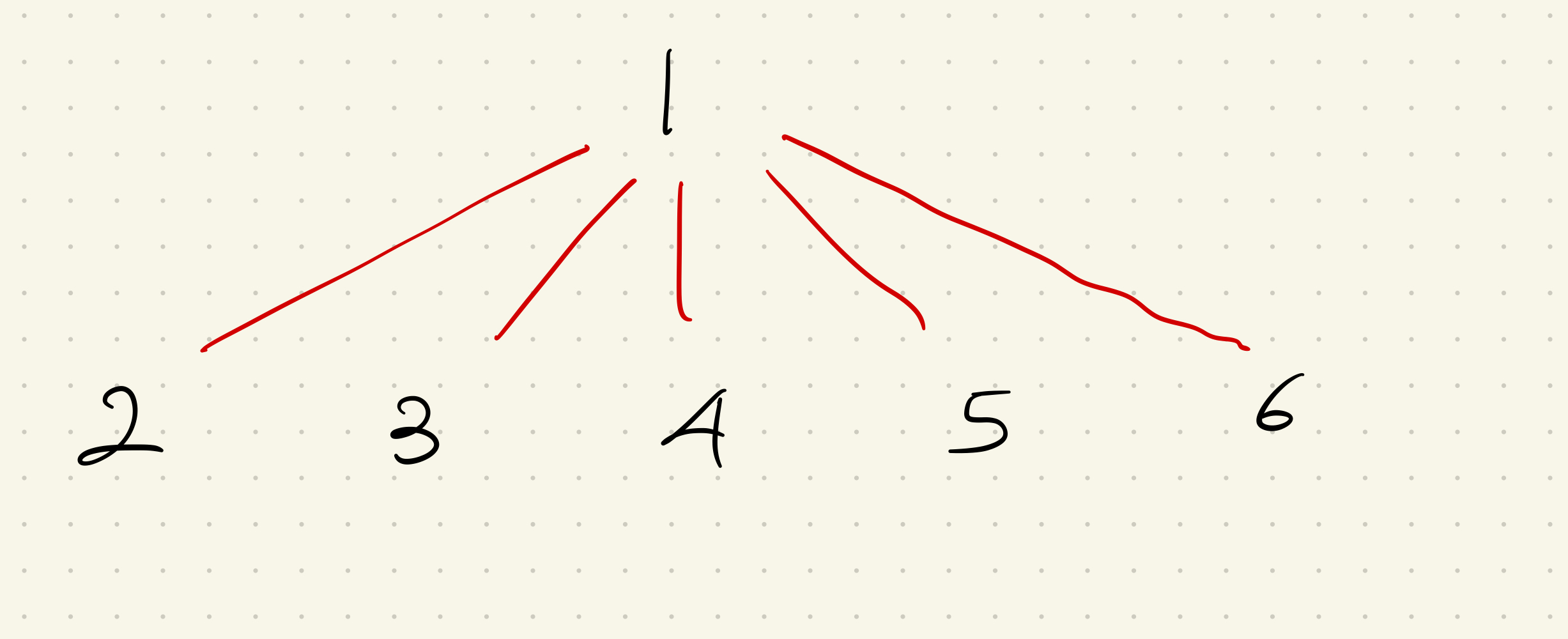
유니온 파인드 알고리즘에선 사실 특정 노드의 부모를 정확하게 알 필요가 없다.

임의의 노드가 어떤 노드에 포함되어 있는지 알기만 하면 되기 때문이다. 위의 예시에서

6은 부모가 5이지만, 궁극적으로는 1에 포함되어있는 노드이기 때문에 사실상 1이 부모라고 해도 별 상관은 없다.(이 논리는 오직 유니온-파인드 알고리즘에서만 유효하다.)

즉 위의 그래프는 다음과 같이 변경 가능하다.

이런 그래프의 테이블은 다음과 같다.

0	1	2	3	4	5	6
0	1	1	1	1	1	1

이 table에선 어떤 두 노드를 입력받더라도 단 한번의 과정만 거치면 find가 가능하다.

3. 코드

1717번 : 집합의 표현

import sys
sys.setrecursionlimit(10**5)
read = sys.stdin.readline

n, m = map(int, read().split())
uf = [i for i in range(n+1)]

# 찾기
def find(x):
    if uf[x] != x: # 루트 노드가 아니라면 루트를 찾을때까지 재귀
        uf[x] = find(uf[x])
    
    return uf[x] # 자기 자신이라면 바로 리턴

# 합치기
def union(a, b):
    a = find(a)
    b = find(b)

    if a < b: # 서로 루트가 다르다면
        uf[b] = a
    
    else:
        uf[a] = b

for _ in range(m):
    cal, a, b = map(int, read().split())

    if cal == 0:
        union(a, b)
    
    elif cal == 1:
        root_a = find(a)
        root_b = find(b)

        if root_a == root_b:
            print("YES")
        else:
            print("NO")

전형적인 유니온 파인드 문제이다.
개인적으로 직접 uf talbe을 그려보면서 순서에 따라 변화를 알아보면 이해하기 쉬웠다.