[백준] 재귀, 백트래킹 <2>
#11729 하노이의 탑
하노이의 탑 문제는 대표적인 재귀 알고리즘의 예제이다.
너무나 유명한 문제라 룰을 간단히만 설명하자면 한쪽 탑에 정렬된 원판을 다른 탑으로 옮기는데 이때
- 거쳐갈 수 있는 탑이 하나 있고 (즉 원래 탑, 거쳐갈 수 있는 탑, 목적지 탑. 이렇게 3개의 탑이 있다.)
- 작은 원판 위에 큰 원판을 놓지 못한다.
이런 특징이 있다.
이 문제를 왜 재귀로 풀 수 있는지 간단한 그림과 함께 설명해보겠다.
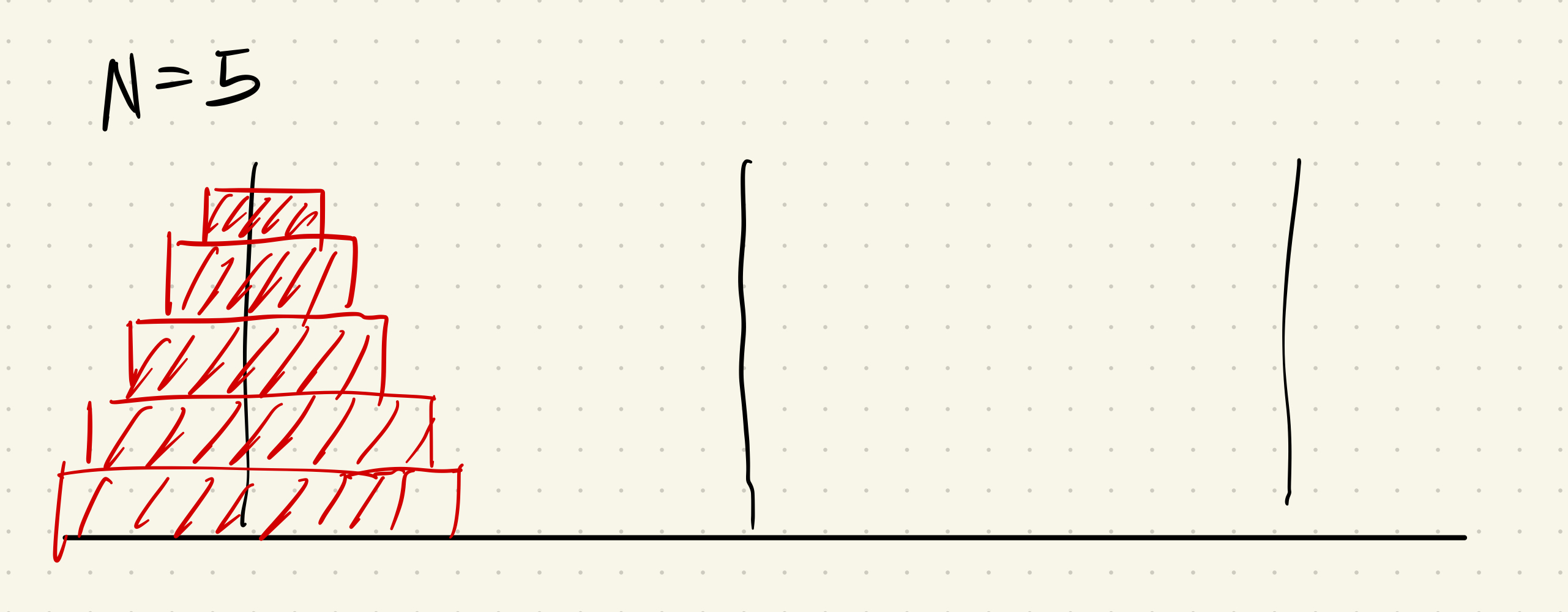
원판이 5개 있다고 생각하고 이때의 초기 상태를 N=5라 하면 다음과 같다.
이때 어떠한 과정을 거쳐서 맨 아래 원판을 목적지 탑으로 이동시키는데 성공하고, 나머지 탑들을 경유지 탑에 쌓았다고 해보자. 그림은 다음과 같다.
(이때의 출발은 1번탑, 경유지는 2번탑, 목적지는 3번탑이다.)
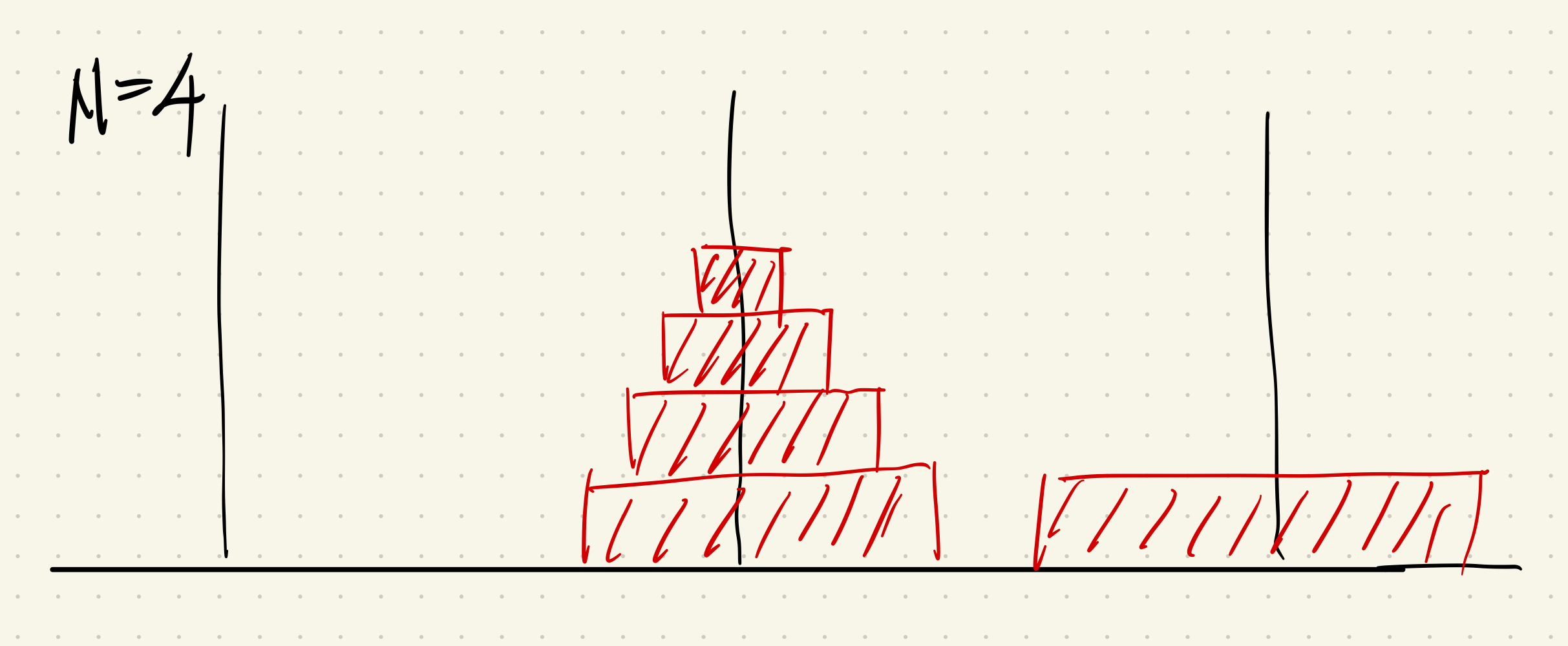
이렇게 되면 원판이 4개 있는 문제와 동일해졌다. 즉 이동 방식을 정해주고 함수 내에서 종료 조건 만 추가해 재귀한다면 코드를 장황하게 작성할 필요가 없는 것이다.
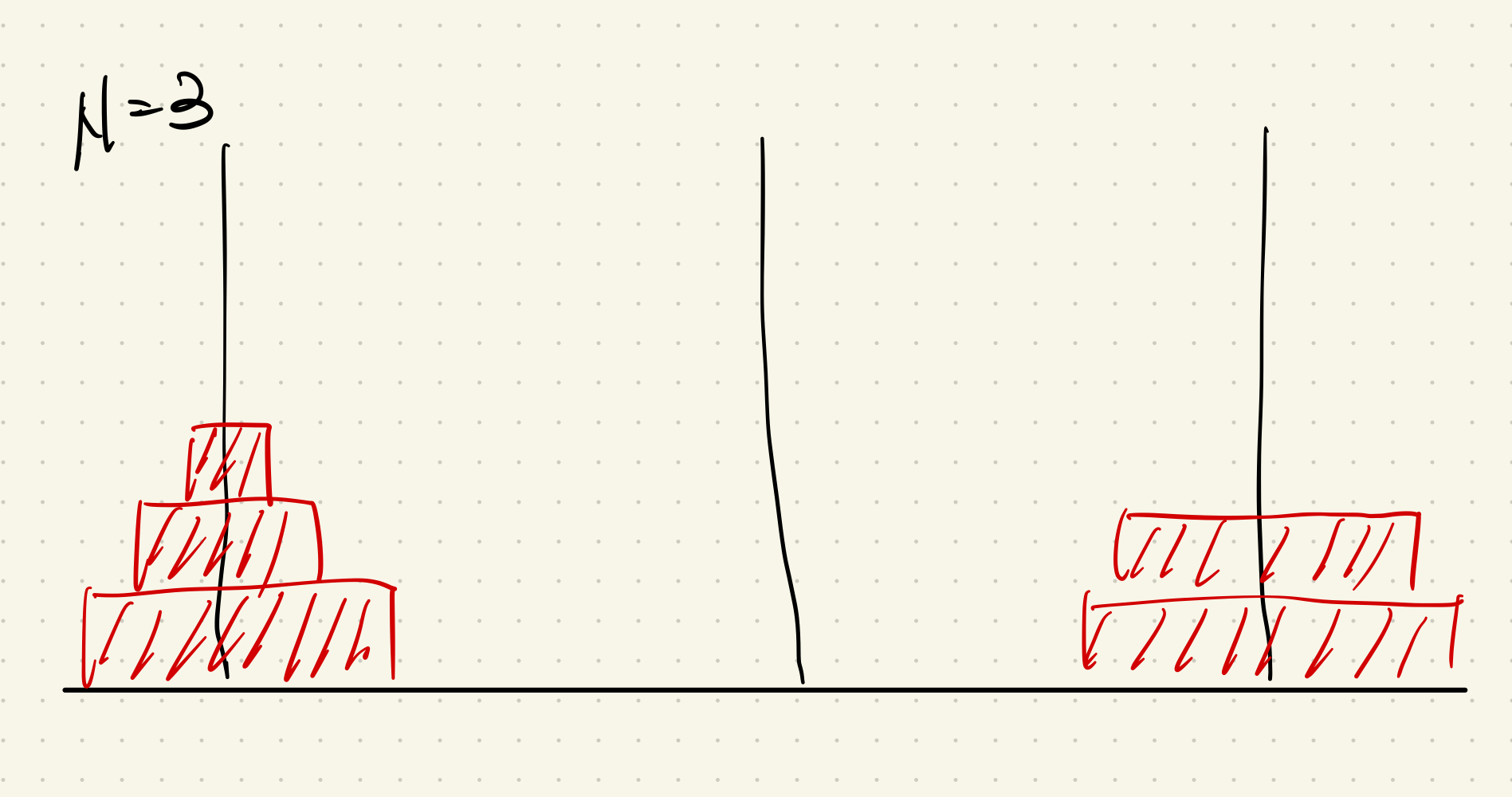
이 상태에서는 경유지 탑을 1번탑, 출발탑을 2번탑, 목적지 탑을 3번탑으로 해준다면 다시 원탑이 3개인 문제와 같아진다.
작성한 내용을 토대로 우리에게 필요한 것은 다음과 같이 정리할 수 있다.
- 하노이 함수
- 원판의 갯수
- 원판의 이동 방식
- 종료조건
- (추가) 목적지와 도착지 출력
마지막 필요사항은 백준 문제에서 요구하는 사항이기 때문에 추가했다.
하노이 함수에 들어갈 매개변수는 원판 갯수, 출발지, 경유지, 목적지 이다.
또한 코드 상에서 실제로 탑을 이동시켜 줄 필요는 없다. (예를 들어 3개의 리스트를 준비해 숫자의 대소를 비교한 후 이동) 재귀할때 원판의 갯수를 하나씩 줄여나가면 된다.
하노이 함수의 종료조건은 원판 갯수가 하나 가 될 때이다. 이때는 한번만 이동하면 되기 때문이다. 이때 마지막 이동 경로를 출력하고 종료하면 된다.
종료 조건이 아닌 경우엔
- 시작 시 가장 밑에 있는 원판을 제외한 갯수 - 1 개의 원판을 경유지 탑을 목적지로 정하고 (즉 목적지 탑이 경유지 탑) 이동한다. (이 재귀가 끝난다면 종료조건을 만족해 마지막 남은 가장 큰 원판은 자동으로 목적지 탑으로 이동한다.)
- 1번의 재귀가 끝난다면 n = 4 의 사진과 같은 경우일 것이다. 이 때에는 갯수 - 1개의 원판을 시작 탑을 경유탑으로 지정한 후 목적지 탑으로 이동한다. 위와 동일하게 마지막 남은 판은 자동으로 이동한다.
- 위의 2번의 재귀가 끝난다면 n = 3의 그림과 같을 것이다.
즉 hanoi 함수 안에서 2번의 재귀가 일어나야 한다.
코드로 작성한다면 다음과 같다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import sys
count = int(sys.stdin.readline().strip())
def move(start, destination): # 출발지와 도착지를 출력하기 위한 함수
print(start, destination)
def hanoi(count, start, destination, via): ## 원판수, 출발지, 목적지, 경유지
if (count == 1):
return move(start,destination)
elif (count != 1):
hanoi(count - 1, start, via, destination) ## n-1개의 원판을 경유지 기둥으로 이동
move(start,destination)
hanoi(count - 1, via, destination, start) ## n-1개의 원판을 시작 기둥으로 이동
print(2**count - 1)
hanoi(count,1,3,2)