[백준] 그리디 알고리즘 <1>

게시 2024/05/30

By Yu.S.H 13 분읽는 시간

1. Greedy 알고리즘 설명

그리디 알고리즘은 매 순간 최적의 선택을 하는 결정이 전체의 관점에서도 최적의 선택인 알고리즘이다.

예를 들어 A - > B → C → D 의 루트로 A에서 출발해 D로 도착하려 할 때, A → B, B → C, C → D의 각각의 루트를 언제나 가장 짧은 경로로 이동해야만 전체 경로에서도 가장 짧은 거리가 된다.

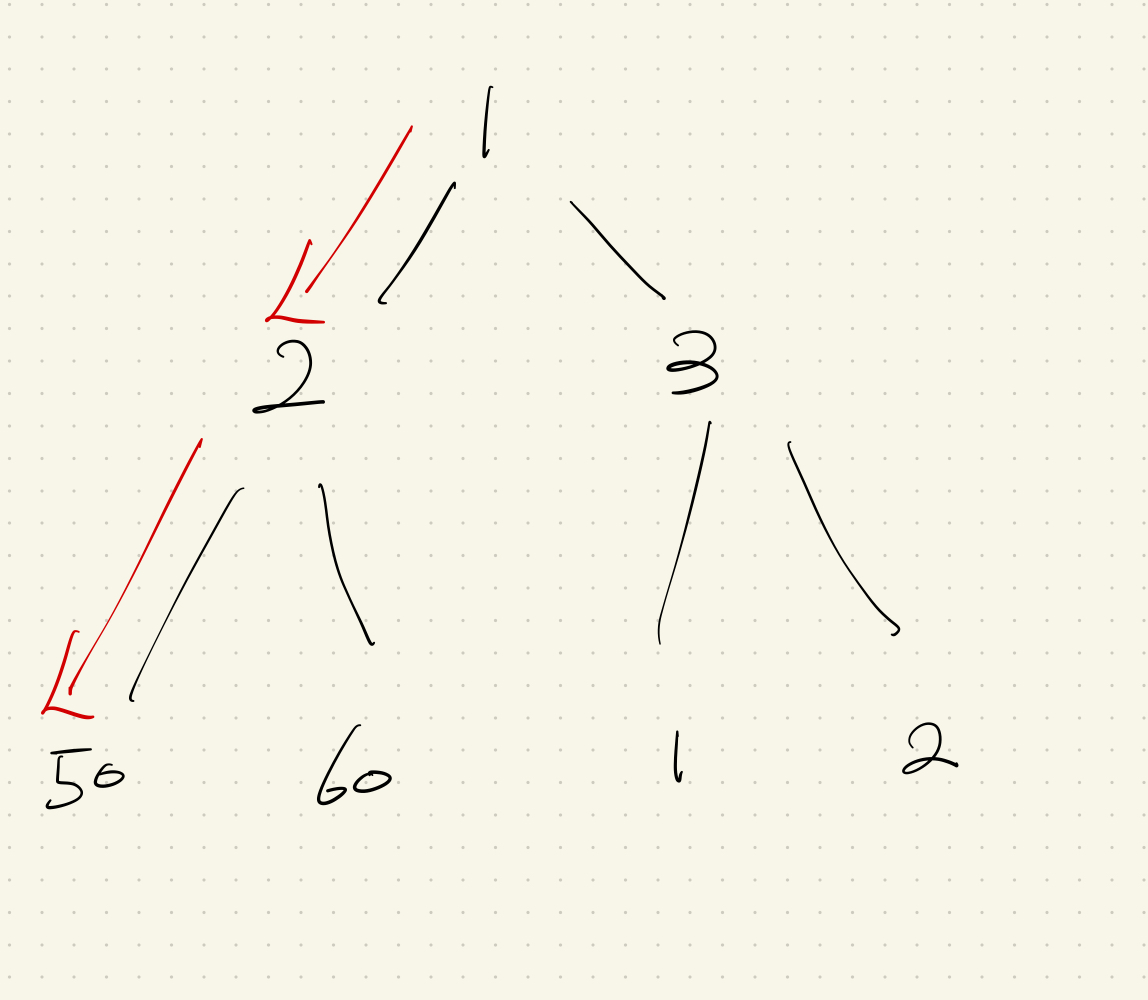
그렇기 때문에 그리디 알고리즘은 각각의 선택이 이전 선택에 영향을 받아서는 안 된다. 예를 들어 트리에서 가장 작은 합의 루트를 찾는다고 해보자.

그리디 알고리즘으로 따라간다면 1 → 2 → 50 이 된다.

이 경우엔 1에서 2와 3을 고르는 과정에서 골라지지 않은 선택지의 이후 가능성은 모두 무시되기 때문에 이전 선택이 영향을 받는다고 본다. (즉 1 → 3 → 1 의 선택지가 무시되었다.) 이런 문제에서는 그리디 알고리즘이 적당하지 않다.

2. Greedy 알고리즘 문제

직접 풀어본 그리디 알고리즘의 문제들은 특정한 발상을 요구하는 경우가 많았다. 해당 유형의 문제들을 많이 풀어보아야 빨리 판단할 수 있다고 생각했다.

특히 정렬을 요구하는 경우가 많기 때문에 Greedy 문제라고 판단되면 정렬, heapq를 사용할 것을 고려하자.

2.1 ATM

백준 11399번: ATM

실버 4 난이도의 그리디 알고리즘 입문 문제이다.

사람들이 돈을 인출하는 시간이 리스트로 주어지고, 이때 각 사람들이 돈을 인출하는데 필요한 시간의 합의 최소를 구하는 문제이다.

예를 들어 [2, 1, 3, 4, 5] 가 주어졌다고 해보자.

첫 번째 사람은 2분을 기다린다.

두 번째 사람은 2 + 1, 3분을 기다린다.

세 번째 사람은 3 + 3, 6분을 기다린다.

네 번째 사람은 6 + 4, 10분을 기다린다.

다섯번째 사람은 10 + 5, 15분을 기다린다.

이때 모든 사람이 기다린 시간의 총 합은 2 + 3 + 6 + 10 + 15 가 된다. 이 시간을 최소로 만들어야 한다.

간단한 문제이다. 먼저 인출 할수록, 기다린 시간의 총합에서 그 시간이 누적된다. 즉 가장 짧은 시간이 걸리는 사람이 먼저 인출한다면 최소값을 구할 수 있다.

  
import sys
read = sys.stdin.readline

people = int(read())
timeList = list(map(int,read().split()))

timeList.sort()

prefixList = [0]
answer = 0

for idx in range(len(timeList)):
    prefixSum = prefixList[idx] + timeList[idx]
    prefixList.append(prefixSum)
    answer += prefixSum

print(answer)

2.2 카드 정렬하기

백준 1715번: 카드 정렬하기

N개 묶음의 카드뭉치가 주어지고, 각각의 뭉치의 카드 수 만큼 비교를 한 후 합친다. 모든 묶음의 카드를 하나로 합쳤을 때 가장 최소의 비교를 구하는 문제이다.

10, 20, 40의 뭉치가 주어졌다면, 10과 20을 비교해 30번 비교한다. 그 다음 30의 뭉치와 40의 뭉치를 비교해 70번 비교한다.

이 경우 30 + 70 번 비교했으므로 횟수는 100회가 된다.

ATM 문제를 먼저 풀어봤다면, 비교적 쉽게 해결 방안을 도출할 수 있다. 다른 점은 이 문제에선 2개의 뭉치를 같이 비교해야 한다는 점이다.

주어진 N개 카드에서 가장 작은 뭉치 2개를 뽑는다. 그것들의 비교 횟수를 계산하고 합친 후 다시 리스트에 집어넣는다.

이 과정을 N-1 회 반복해주면 된다. 카드를 뽑고 합치고 다시 집어넣을때 마다 정렬을 한다면 시간복잡도에서 많은 손해를 볼 수 있으므로 heapq를 사용한 우선순위큐를 활용하면 좋다.

  
import sys
import heapq
read = sys.stdin.readline

N = int(read())
pq = []

for _ in range(N):
    num = int(read())
    heapq.heappush(pq, num)

counts = []

def sort_cards(N):
    for _ in range(N-1):
        num1 = heapq.heappop(pq)
        num2 = heapq.heappop(pq)

        result = num1 + num2
        heapq.heappush(pq, result)
        counts.append(result)

sort_cards(N)

print(sum(counts))

최소 우선순위 큐를 사용한다면 항상 가장 작은 값 2개를 뽑을 수 있기 때문에 반복문을 사용하기 용이하다.

2.3 과제

백준 13904번: 과제

개인적으로 발상을 찾기 쉽지 않은 문제였다.

현재로부터의 과제 마감일이 주어지고, 그 과제의 점수가 주어진다. 하루에 하나의 과제밖에 제출할 수 없다고 할 때, 가장 많은 점수를 받도록 하는 것이 문제이다.

이 문제는 가장 높은 점수를 가진 과제를 마감일에 제일 임박해서 제출하게 배치하면 된다. 만약 마감일에 다른 과제가 배치됐을 경우, 하루하루 앞당기면서 배치한다. 예시를 보자.

(d, p), d: 과제마감일, p: 점수 로 주어질 때, 과제들을 최대 큐를 사용해 점수 기준으로 정렬한다.

최대 큐 = [(4, 60), (2, 50), (4, 40), (3, 30), (1, 20), (4, 10), (6, 5)]
이때 스케쥴 리스트를 만들고, 각각의 인덱스를 날짜로 잡아준다.
0 1 2 3 4 5 6
0 0 0 0 0 0 0
이때 0번 인덱스는 0일이 없기 때문에 값이 들어오지 않는 더미 인덱스다.
점수가 높은 순서대로 해당 날짜의 인덱스가 비어있을 경우 배정한다.
최대 큐 = [(4, 40), (3, 30), (1, 20), (4, 10), (6, 5)]
0 1 2 3 4 5 6
0 0 50 0 60 0 0
다음 항목인 4일 40점의 경우 4일이 이미 배정되어있기 때문에, 해당 데드라인부터 하루씩 줄여 비어있는 곳에 배치한다.
0 1 2 3 4 5 6
0 30 50 40 60 0 0
최대 큐 = [(1, 20), (4, 10), (6, 5)]
1일 20점, 4일 10점의 과제들은 더 이상 배치될 날짜가 없으므로 배치하지 않는다.
완성된 후 스케쥴 리스트는 다음과 같다
0 1 2 3 4 5 6
0 30 50 40 60 0 5
가장 높은 점수는 185점 이다.

0	1	2	3	4	5	6
0	0	0	0	0	0	0

0	1	2	3	4	5	6
0	0	50	0	60	0	0

0	1	2	3	4	5	6
0	30	50	40	60	0	0

0	1	2	3	4	5	6
0	30	50	40	60	0	5

  
import sys
import heapq
read = sys.stdin.readline

N = int(read())
max_pq = []
schedules = [0 for _ in range(1001)]

# d: 과제마감일
# w: 과제 점수
# 하루에 한 과제 수행 가능

for _ in range(N):
    d, w = map(int,read().split())  
    heapq.heappush(max_pq,(-w ,d))

while max_pq:
    score, due = heapq.heappop(max_pq)
    
    if schedules[due] == 0: # 비어있다면
        schedules[due] = -score
    else: # 비어있지 않다면
        while True:
            due -= 1
            if due <= 0:
                break
            if schedules[due] == 0:
                schedules[due] = -score
                break

    
print(sum(schedules))

2.4 강의실

백준 1374번: 강의실

개인적으로 발상이 어려운 문제였다.

강의들의 시간이 주어지고, 한 강의실에선 한 가지 강의밖에 이루어지지 못한다. 이때 필요한 최소 강의실 숫자를 구하는 문제이다.

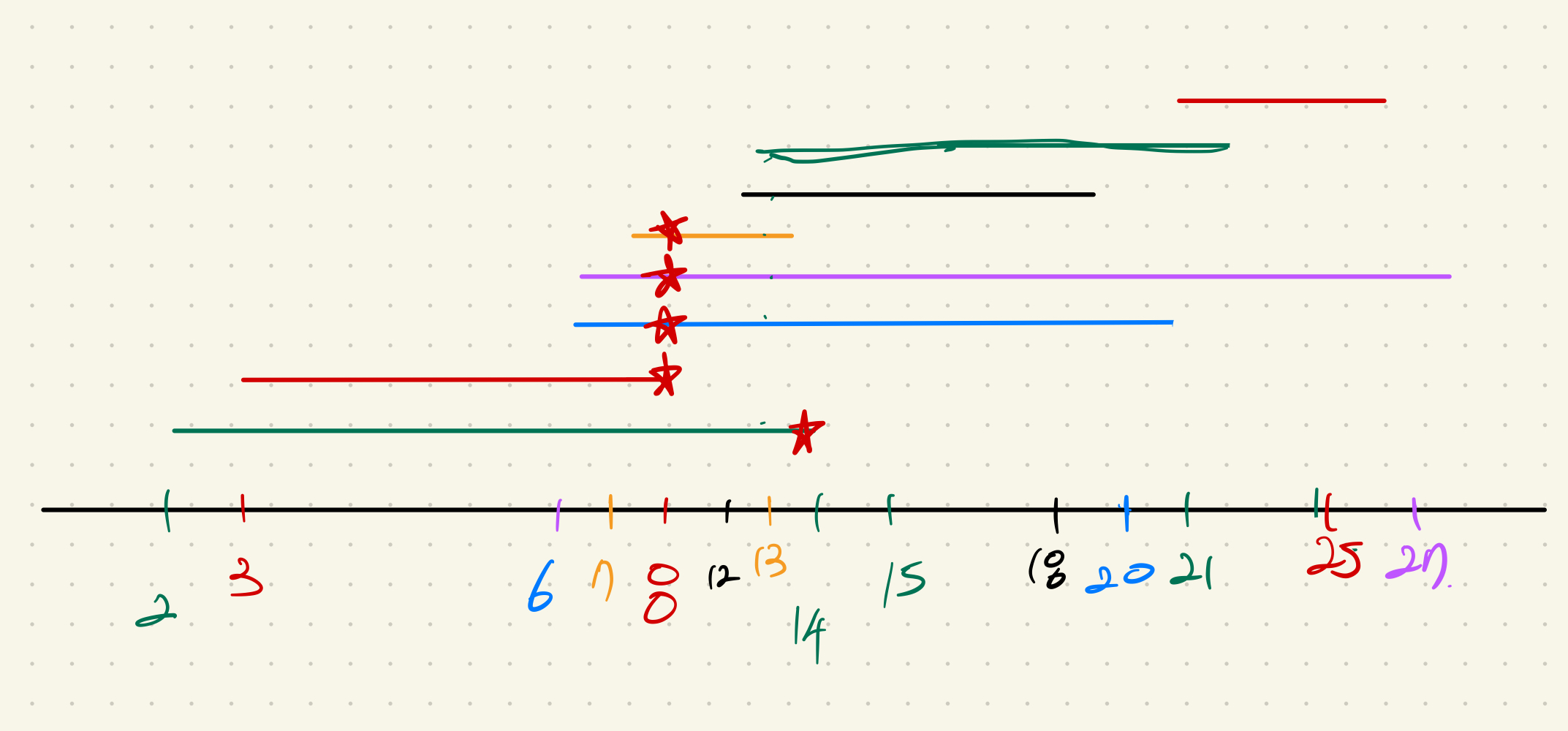
즉 강의들이 가장 많이 겹치는 숫자를 구하는 문제이다. 그림을 그려 문제를 풀어보자. 강의들을 시작시간이 빠른 순으로 정렬하면 다음 그림과 같다.

가장 시작시간이 빠른 강의의 종료시간을 찾아 큐에 넣어준다.
이 때는 2시에 시작하고 14시에 끝나는 경우이므로
pq = [14]
시작시간 순으로 정렬한 강의들을 순서대로 비교하면서 pq에서 가장 빠른 종료시간보다, 비교할 강의의 시작시간이 작다면(겹친다면) pq에 추가한다.
pq에서 가장 빠른 종료 시간보다 비교할 강의의 시작시간이 크다면 heappop으로 가장 작은 요소 제거 후, 현재 강의의 종료시간을 추가.
2, 3번을 반복한다.

그림에서 마저 진행한다면 다음 비교할 강의의 진행시간은 3 ~ 8 이므로 3이 14보다 작다. 이때 8을 추가한다. pq = [8, 14]

다음은 6 ~ 20. 6이 8보다 작다. 20을 추가한다. pq = [8, 14, 20]

다음은 6 ~ 27. 6이 8보다 작다. 27을 추가한다. pq = [8, 14, 20, 27]

다음은 7 ~ 13. 7이 8보다 작다. 13을 추가한다. pq = [8, 13, 14, 20, 27]

다음은 12 ~ 18. 12가 8보다 크므로 8을 제거 후 18을 추가한다 pq = [13, 14, 18, 20, 27]

이 과정을 반복한 후 마지막 남은 pq의 길이가 가장 많이 겹쳤던 강의의 숫자가 된다.

  
import sys
import heapq
read = sys.stdin.readline

N = int(read())

schedules = []
for _ in range(N):
    num, start, end = map(int,read().split())
    schedules.append((start, end))

schedules.sort()
pq = [schedules[0][1]] # 가장 먼저 시작하는 강의의 종료시간

for i in range(1, N):    
    if pq and pq[0] > schedules[i][0]:
        heapq.heappush(pq, schedules[i][1])
    else:
        heapq.heappop(pq)
        heapq.heappush(pq, schedules[i][1])

print(len(pq))

단순히 최대로 겹쳤던 갯수만 구하는 문제이기 때문에 어느 강의가 들어가고 빠지는 것은 중요하지 않다.

Algorithm