[백준] 세그먼트 트리(Segment Tree)
1. 세그먼트 트리 소개
세그먼트 트리(Segment Tree)는 트리에 속한 자료구조 중 하나로, 주로 배열 내의 범위에 대한 질의에 대해 사용한다. 주요 사용처는 아래와 같다.
전제조건: 리스트가 주어진다. ex) [1,2,7,6,9,4,66,9,1,…] 주어진 리스트에서 이하의 값을 구할 때 사용된다.
- 구간 질의: 주어진 범위 내의 합, 곱, 최대값, 최소값 등등 구하기.
- 구간 업데이트: 위의 구간 질의를 수행할 수 있으면서, 동시에 특정 인덱스의 숫자 바꾸기.
1.1 세그먼트 트리 사용 이유
단순히 여기까지만 들으면 굳이 불편하게 자료구조를 사용하지 않고 슬라이싱 한 뒤, max 혹은 min 함수를 쓰는 것도 나쁘지 않아보인다.
하지만 배열에서 구간질의(구간 내의 합, 최대값, 곱, 최소값 등)을 구하기 위해선 $O(N)$의 시간 복잡도가 소요된다. 당연히 배열의 크기가 커지면 시간 내로 처리하지 못할 수도 있다.
이를 해결하기 위해 세그먼트 트리를 사용한다. 세그먼트 트리는 구간 질의를 $O(logN)$ 에 처리 가능하다.
1.2 세그먼트 트리의 구조
세그먼트 트리는 배열 내 원하는 값을 트리의 형태로 저장해 놓는 구조다. 예를 들어서 길이가 6인 리스트가 주어지고, 구간 내의 최소값을 구한다고 가정해보자.
주어진 리스트 = [10, 9, 8, 7, 6, 5]
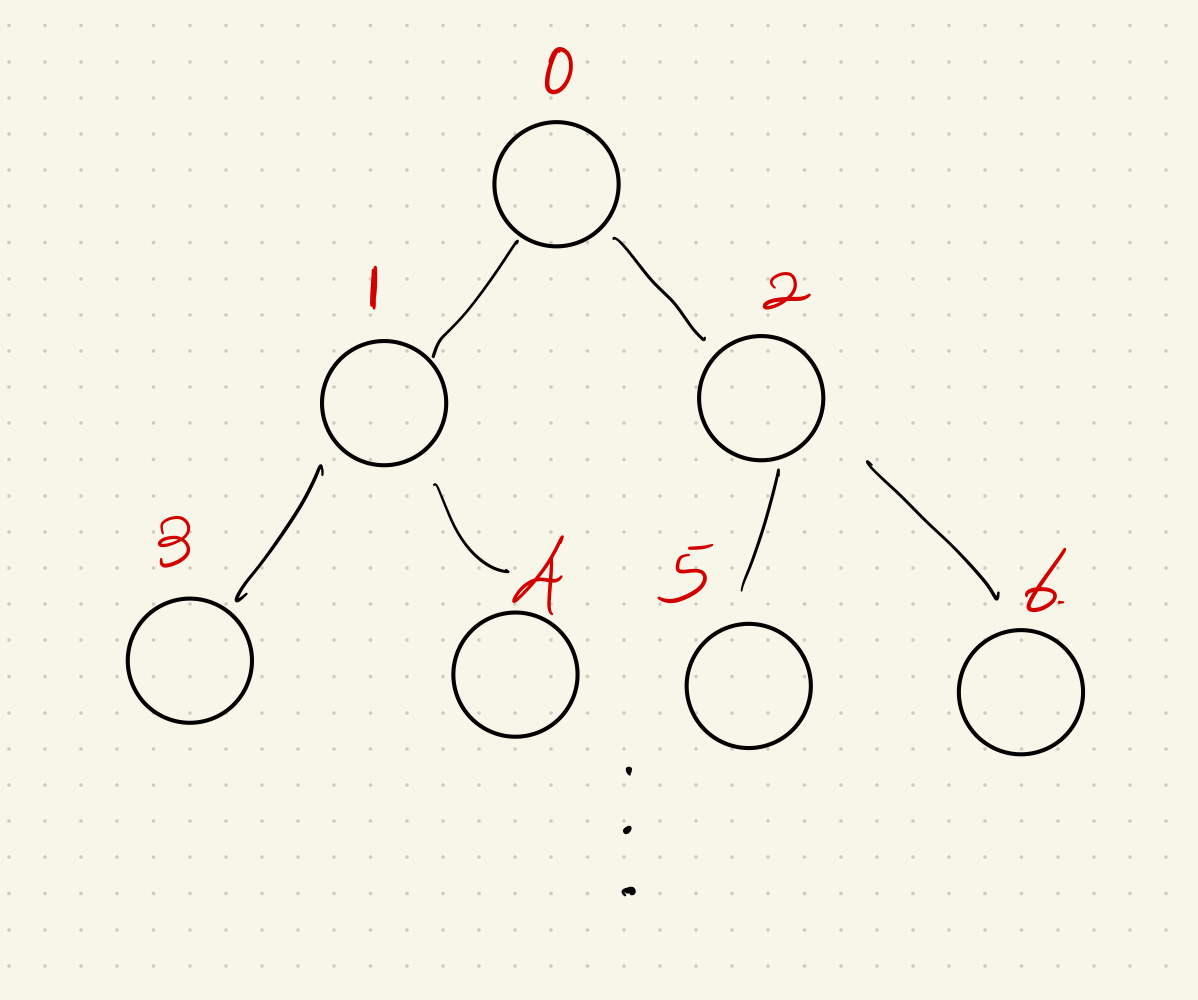
세그먼트 트리는 다음과 같이 구성된다. 일반적으로 세그먼트 트리는 넉넉하게 구성되기 때문에, 주어진 리스트의 4배의 길이로 만들어놓는다.
붉은색 숫자는 세그먼트 트리의 인덱스이다.
세그먼트 트리 내의 값은 다음의 규칙에 의해 구성된다.
- 세그먼트 트리 0번 인덱스에는 데이터의 0번 ~ 5번 인덱스의 최소값이 들어간다.
- 세그먼트 트리 1번 인덱스에는 데이터의 0번 ~ 2번 인덱스의 최소값이 들어간다.
- 세그먼트 트리 2번 인덱스에는 데이터의 3번 ~ 5번 인덱스의 최소값이 들어간다.
…
즉 왼쪽 트리에는 범위 반으로 갈라 왼쪽 범위 내의 값을 저장하고, 오른쪽 트리에는 오른쪽 범위 내의 값을 저장한다.
가장 마지막 세그먼트 트리 노드에는 리스트의 값을 넣는다.
이 작업을 재귀로 구성한다.
트리에 값을 넣는다면 다음과 같다.
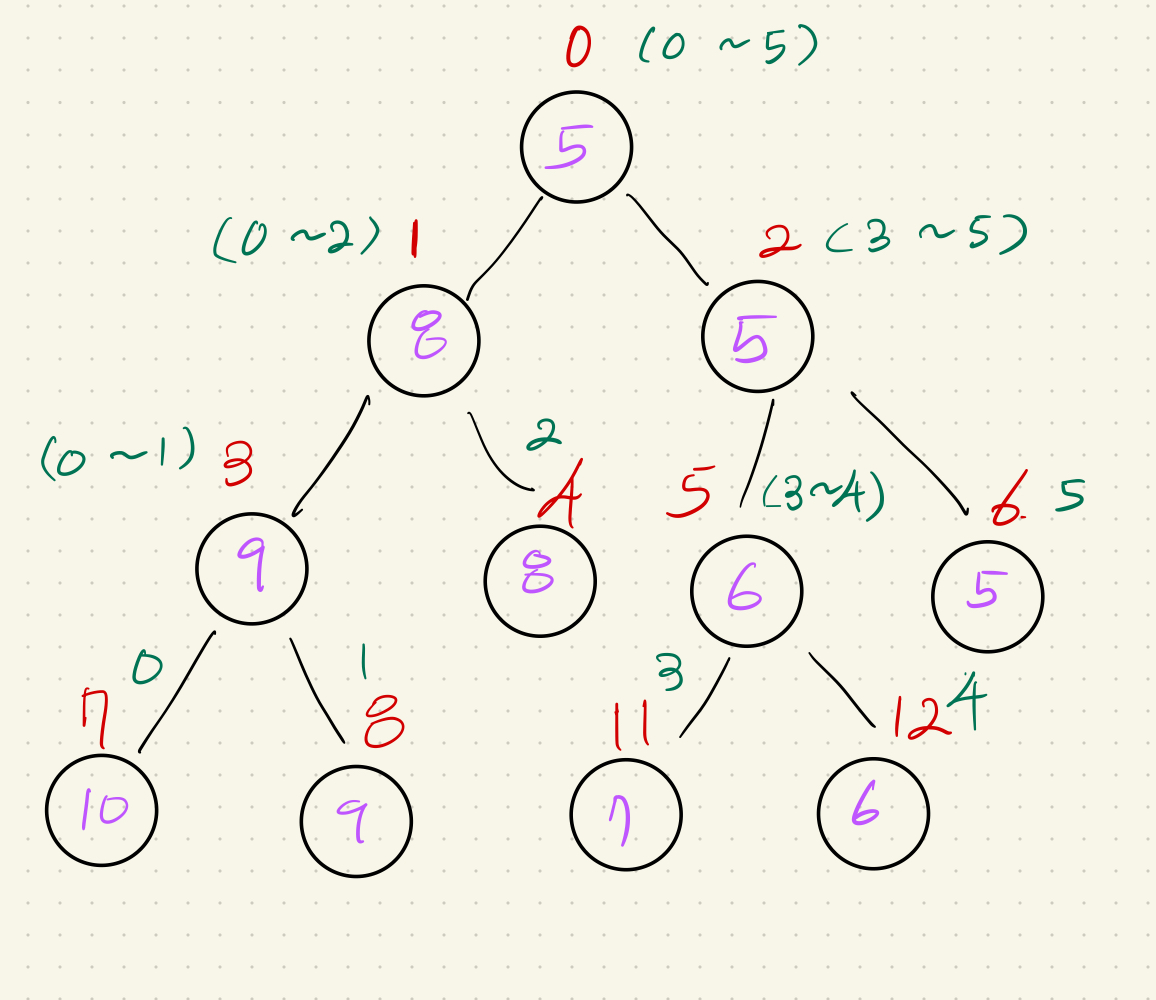녹색 숫자: 해당 세그먼트 트리에 들어갈 범위
보라색 숫자: 세그먼트 트리의 값
2. 코드
세그먼트 트리가 여러 작업을 하기 때문에 클래스로 구현하면 관리하기 편하다.
2.1 세그먼트 트리 클래스 초기화
1
2
3
4
5
6
7
class SegmentTree:
# array: 주어지는 배열
def __init__(self, array):
self.data = array
self.n = len(array)
self.sum_tree = [0] * (4*self.n)
self.build(0, 0, self.n-1)
세그먼트 트리를 만들 때, 가장 처음 구성되게 한다. 이때 세그먼트 트리의 배열 크기는 주어진 배열의 4배로 한다.
build 함수는 클래스 내부함수로, 주어진 배열을 세그먼트 트리에 집어넣는 작업을 한다.
2.2 세그먼트 트리 값 할당
각 세그먼트 트리 인덱스에 알맞은 값을 할당한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
def build(self, node, start, end):
# 재귀를 돌다가 리프노드에 도착하면, 값 할당
if start == end:
self.sum_tree[node] = self.data[start]
else:
mid = (start+end) // 2
left = 2 * node + 1
right = 2 * node + 2
self.build(left, start, mid)
self.build(right, mid+1, end)
self.sum_tree[node] = self.sum_tree[left] + self.sum_tree[right]
기본적으로 재귀함수 꼴을 사용해 값을 집어넣는다.
리프 노드라면 값을 할당한다.
리프 노드가 아니라면 범위를 반으로 나눠 재귀한다.
부모 노드에 원하는 값을 집어넣는다. (이 예시에선 범위 합을 구현했다.)
2.3 구간 질의
핵심 기능인 구간 질의 기능이다. 구간이 주어지면, 그 구간에 해당하는 값을 불러온다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def find_sum_value(self, L, R):
return self._query(0,0, self.n-1, L, R)
def _query(self, node, start, end, L, R):
if R < start or L > end:
return 0
if L <= start and R >= end:
return self.sum_tree[node]
mid = (start+end) // 2
left = 2*node+1
right = 2*node+2
left_sum = self._query(left, start, mid, L, R)
right_sum = self._query(right, mid+1, end, L, R)
return left_sum + right_sum
외부에서 find_sum_value 를 호출하면, 내부에서 _query 함수를 호출하게 구성했다.
주어진 구간의 경우의 수는 다음과 같다.
- 질의로 주어진 구간의 범위가 찾고있는 구간의 범위와 겹치지 않는 경우
- 질의로 주어진 구간의 범위가 찾고있는 구간의 범위와 완전히 겹치는 경우
- 질의로 주어진 구간의 범위가 찾고있는 구간의 범위와 일부분만 겹치는 경우
1의 경우는 첫번째 if문에서 해결한다. 겹치지 않는다면 더해도 영향이 없게 0을 리턴한다. (예를 들어 구간곱이라면1, 구간 최소값이라면 math.inf…)
2 경우는 두번째 if문에서 해결한다. 찾고있는 범위가 질의와 완전히 겹친다면 단순하게 노드의 값을 불러오면 해결된다.
3의 경우는 그 이하에서 해결한다.
1
2
3
4
5
6
7
8
mid = (start+end) // 2
left = 2*node+1
right = 2*node+2
left_sum = self._query(left, start, mid, L, R)
right_sum = self._query(right, mid+1, end, L, R)
return left_sum + right_sum
구간을 반으로 나눈 후, 재귀함수를 사용해 왼쪽 합과 오른쪽 합을 따로 구한다.
2.4 구간 업데이트
핵심 기능인 구간 업데이트다. 세그먼트 트리의 구조를 깨지 않고 구간을 찾아 업데이트한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def update(self, target, value):
return self._update_value(0, 0, self.n-1, target, value)
def _update_value(self, node, start, end, target, value):
if start == end: # 리프 노드면 값 업데이트
self.sum_tree[node] = value
self.data[start] = value
else:
mid = (start+end) // 2
left = 2*node+1
right = 2*node+2
if target <= mid: # 타겟 인덱스가 mid보다 작다면 왼쪽에서 찾기
self._update_value(left, start, mid, target, value)
else:
self._update_value(right, mid+1, end, target, value)
self.sum_tree[node] = self.sum_tree[left] + self.sum_tree[right]
위의 세그먼트 트리의 값을 할당하는 함수와 비슷한 구조이다. 범위를 찾아, 리프노드면 값을 업데이트, 아니라면 반으로 나누어서 재귀함수로 찾는다.
3. 문제
기본적으로 세그먼트 트리의 코드 양이 길고, 복잡한 자료구조이다 보니 백준에서 높은 난이도의 문제들을 가지고 있다.