[백준] DP <1>
동적 프로그래밍 (Dynamic Programing)
동적 프로그래밍이란 이전에 계산한 값을 저장해 둔 후 재활용하는 방법이다. 문제의 주어진 조건에서 점화식을 유도할 수 있다면 동적계획법으로 푸는 것이 효과적이다.
동적 프로그래밍은 이전 값들을 이용하기 때문에 조건에 따라 몇몇 초기 값들은 수동으로 입력해주어야 한다. (초기 값들은 조건에 따라 이전 값이 없을수도 있기 때문이다.)
여담으로 이름과 달리 별로 dynamic한 방법은 아니다.
# 24416 알고리즘 수업 - 피보나치 수 1
피보나치 수는 대표적인 동적 프로그래밍의 예 이다.
피보나치수는 현재 값을 이전 값과 이전이전값의 합으로 나타낼 수 있다. 즉
$fib(n) = fib(n-1) + fib(n-2)$
이다.
점화식에 따라 피보나치 수열의 초기 값은 최소 2개가 필요하기 때문에 fib(0) = 0, fib(1) = 1로 두고 시작해야한다.
특히 피보나치 수열이 동적 프로그래밍의 위력을 보일 좋은 예인 이유는 알고리즘이 비교적 간단하기 때문에 비교하기 쉽다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import sys
number = int(sys.stdin.readline().strip())
dynamicCount = 0
def dynamicFib(num,f = [1,1]):
global dynamicCount
if (num == 1 or num == 2):
dynamicCount += 1
if (num != 1 or num != 2):
for i in range(2,num):
dynamicCount += 1
f.append(f[i - 1] + f[i - 2])
return f[num-1]
target = dynamicFib(number)
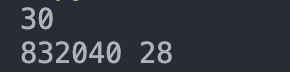
print(target ,dynamicCount)
이때 dynamicCount는 함수의 실행 횟수를 나타낸다.
큰 숫자일수록 동적프로그래밍의 함수 호출 횟수가 압도적으로 작아진다.
같은 문제를 재귀적으로 풀었을 때, 함수 실행횟수를 비교해보자.
1. 재귀함수의 경우.
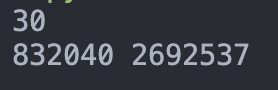
30의 피보나치 수열 값은 832,040이고, 재귀함수의 실행횟수는 2,692,537회 이다.
2. DP의 경우.
같은 30의 경우 실행 횟수가 28회 밖에 되지 않는다.