[백준] 이진트리 순회
1. 이진 트리의 순회방법
1.0 이진 트리 - Binary Tree
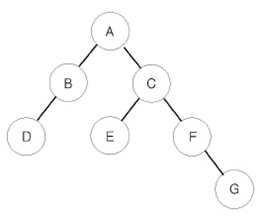
이진 트리는 트리 중에서 각 노드의 자식 노드가 최대 2개인 노드를 뜻한다. 때문에 자식 노드가 없을수도, 하나만 있을수도, 2개까지 있을수도 있지만 3개 이상의 자식노드를 갖지 않는다.
특이점으로는 왼쪽 노드와 오른쪽 노드가 구분되어 있으므로 같은 자식 노드라 할지라도 방향이 다르다면 서로 다른 트리이다.
이번 글에서 소개할 이진트리를 순회하는 방식은 3가지이다. 전위 순회(preorder traversal), 중위 순회(inorder traversal), 후위 순회(postorder traversal)
1.1 전위 순회 - preorder traversal
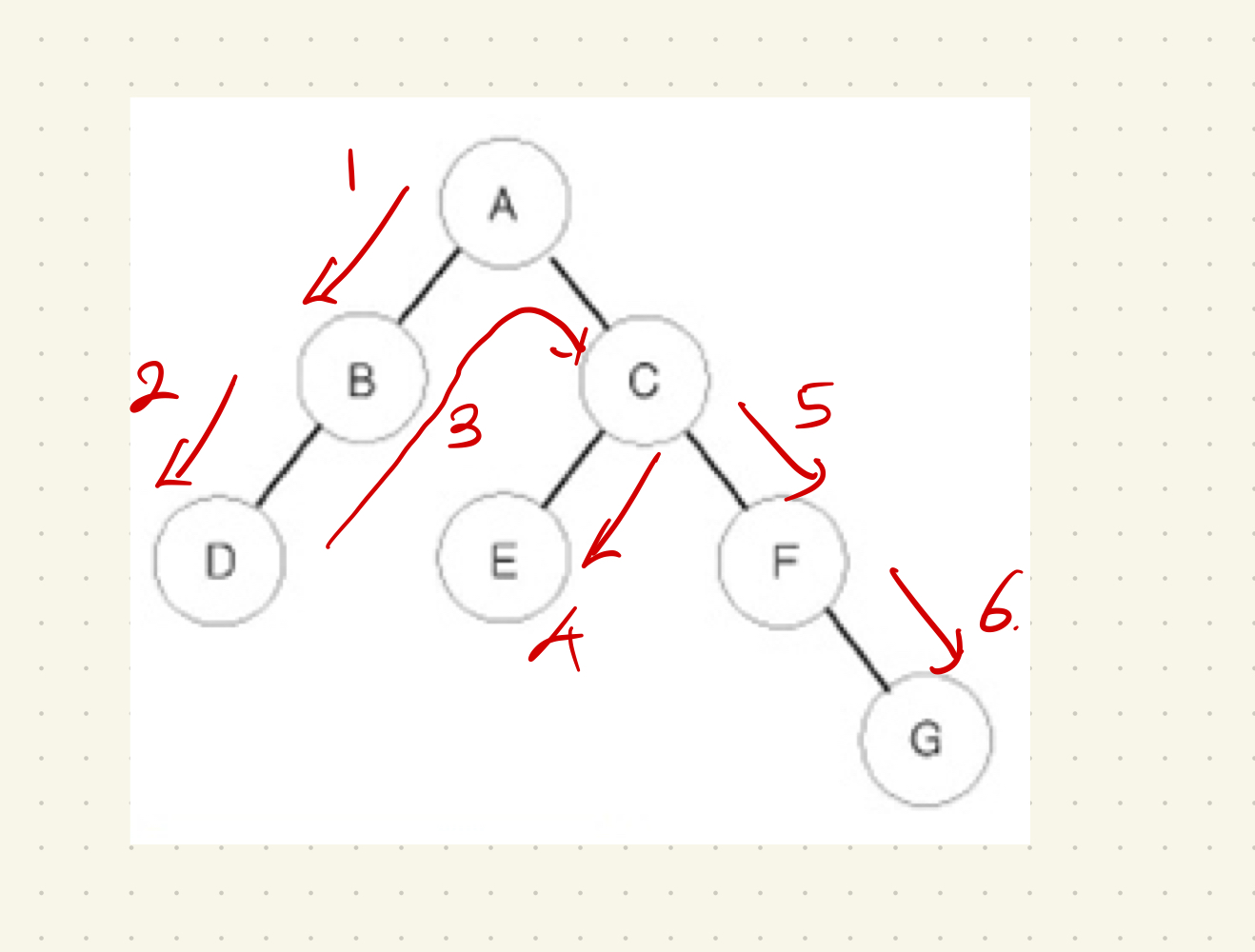
전위순회의 탐색 순서는 root → left → right 이다.
즉 부모노드를 가장 먼저 탐색하고, 자식노드의 왼쪽을 먼저, 그 후 오른쪽을 탐색한다.
왼쪽 노드에 더 이상 탐색할 노드가 없을 경우 부모 노드로 되돌아와 탐색하지 않은 오른쪽 노드를 탐색한다.
탐색 순서를 보면 알겠지만 DFS와 완전히 같은 탐색 순서이다.
1.2 중위 순회 - inorder traversal
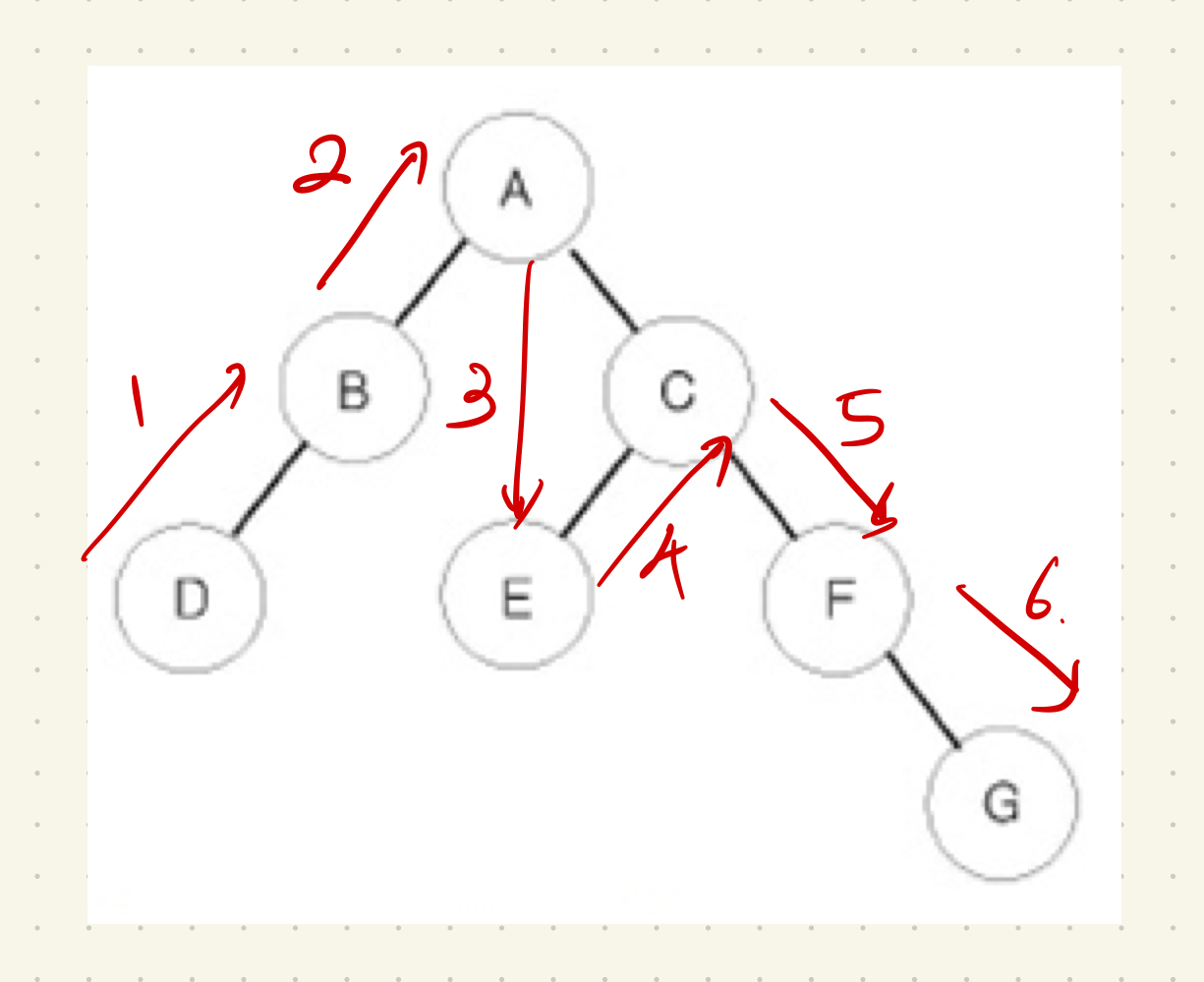
중위순회의 탐색 순서는 left → root → right 이다.
가장 왼쪽 하단의 노드가 먼저 탐색되고 그 부모노드를 다음으로 탐색, 부모노드의 오른쪽 자식 노드를 탐색하면서 나아간다. 더 탐색할 노드가 없다면 부모 노드로 되돌아간다.
1.3 후위 순회 - postorder traversal
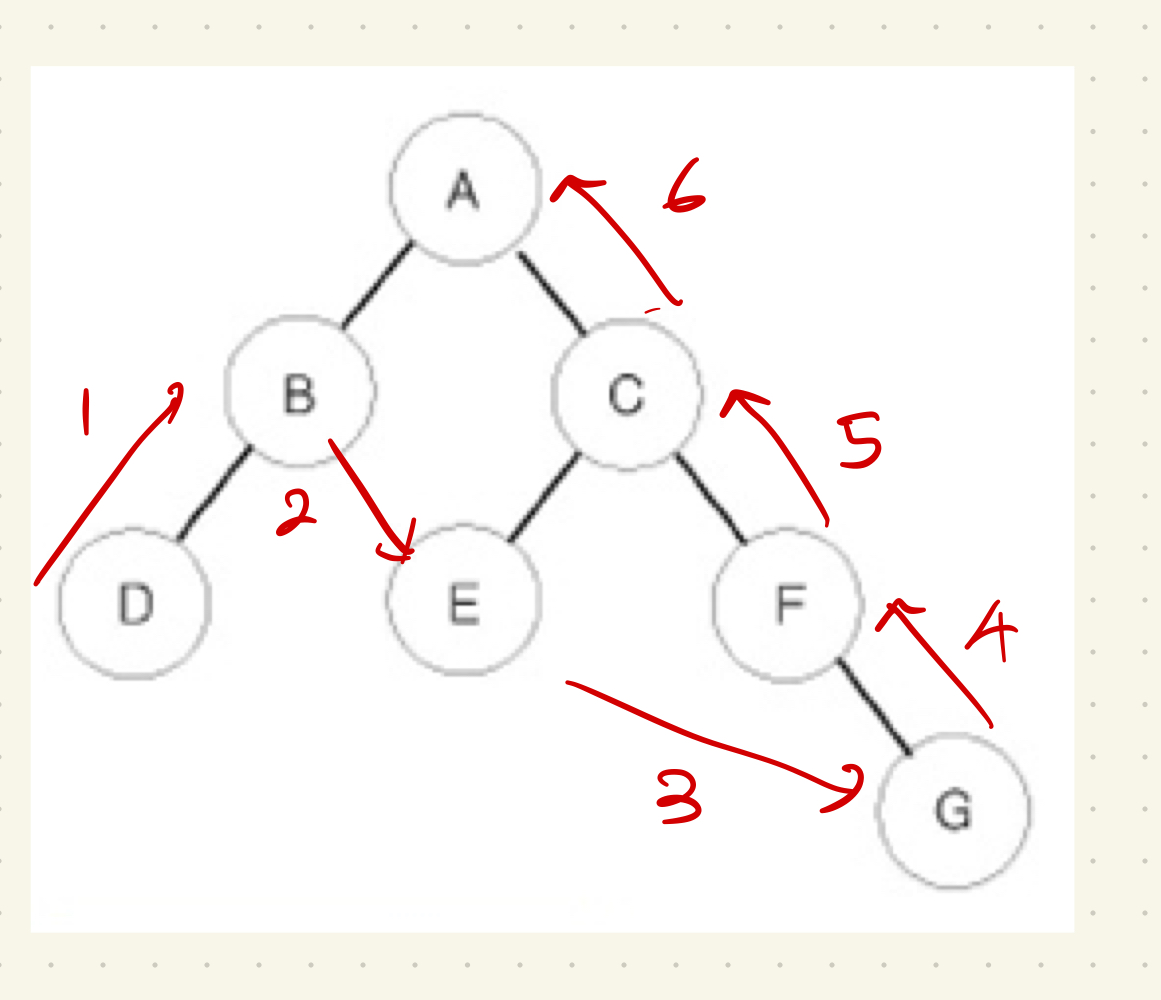
후위순회의 탐색 순서는 left → right → root이다.
부모노드를 최초로 탐색하지 않기 때문에 조금 헷갈릴 수 있다. 이때는 트리를 그려놓고 왼쪽 하단에서 오른쪽 상단으로 지그재그를 그리며 탐색한다고 생각하다면 편하다.
2. 코드
기본적인 이진트리의 각각 순회 순서를 구현할 수 있는지 확인하는 문제이다.
2.0 그래프 구현
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
graph = [[] for _ in range(count+1)] # A = 1, B = 2, ...
def char_to_num(char): # A -> 1, B -> 2, ...
if char == ".":
return None
else:
return ord(char) - 64
def num_to_char(num):
if num == None:
return None
else:
return chr(num+64)
for _ in range(count):
parents, left, right = map(lambda x: char_to_num(x), read().split())
graph[parents].append(left)
graph[parents].append(right)
문제에서 대문자 알파벳을 입력하고 있으므로 정수로 활용하기 위해 ascii code를 활용했다. (A → 1, B → 2, C →3 …)
그 후 graph의 각각의 노드에 왼쪽을 0번 인덱스, 오른쪽을 1번 인덱스에 저장해준다.
2.1 전위 순회
1
2
3
4
5
6
7
8
9
def preorder(next_node):
print(num_to_char(next_node), end = '')
left = graph[next_node][0]
right = graph[next_node][1]
if left:
preorder(left)
if right:
preorder(right)
2.3 중위 순회
1
2
3
4
5
6
7
8
9
def inorder(next_node):
left = graph[next_node][0]
right = graph[next_node][1]
if left:
inorder(left)
print(num_to_char(next_node), end = '')
if right:
inorder(right)
2.4 후위 순회
1
2
3
4
5
6
7
8
9
10
def postorder(next_node):
left = graph[next_node][0]
right = graph[next_node][1]
if left:
postorder(left)
if right:
postorder(right)
print(num_to_char(next_node), end = '')
3. 코드 해설
코드를 보면 놀랄 만큼 간단하다. 이진 트리의 기본적인 움직임(왼쪽을 먼저 탐색 후 오른쪽을 탐색) 을 재귀 함수로 구현한 후, 단순히 print 하는 위치만 조정한다면 각각의 순회 순서를 간단하게 출력할 수 있다.
직접 재귀 함수를 하나씩 뜯어보는것 보다 그림으로 그려 설명하는 편이 간단하다.
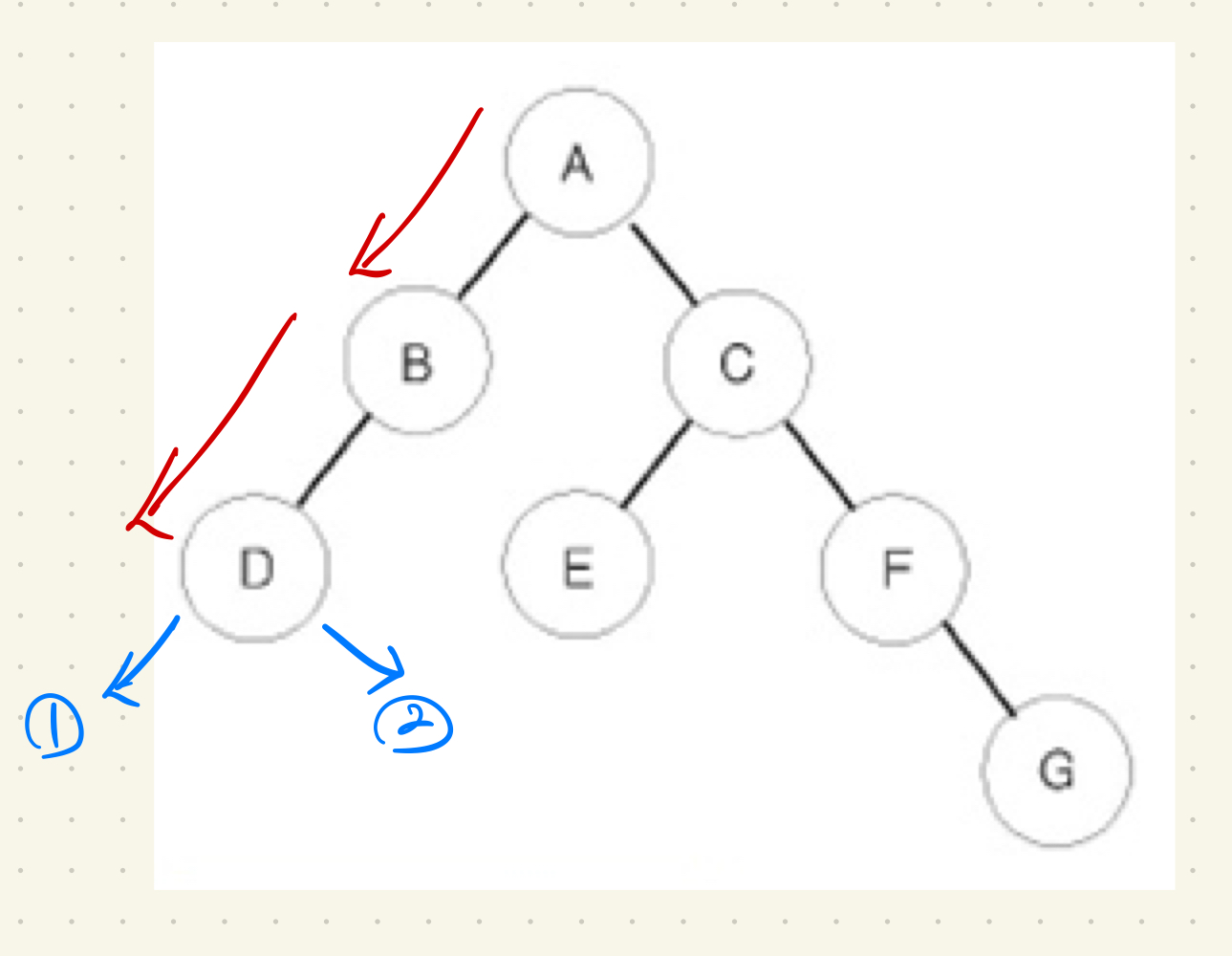
중위순회를 예를 들어 설명해보자. 이때 탐색한 순서를 출력하는 print는 왼쪽과 오른쪽 사이에 있다.
즉 왼쪽 노드의 탐색이 모두 끝난 후 오른쪽을 탐색하려고 시도할 때 해당 노드가 출력된다는 것이다. 이때 오른쪽 노드가 있든 없든 상관이 없다.
이 그림에서 가장 왼쪽인 D 노드를 탐색한 후 D 노드의 가상의 자식노드 1과 2를 탐색하려고 할 것이다. 왼쪽노드 1이 없으므로 오른쪽 노드 2를 탐색하려고 시도할 것이기 때문에 D를 출력한다. 2 노드 역시 없으므로 부모 노드인 B로 되돌아간다.
이때 B 노드에서 오른쪽 노드를 탐색하려고 시도하고, 없으므로 B를 출력 후 부모인 A로 되돌아간다.
A에선 탐색할 오른쪽 노드가 있으므로 A를 출력 후 오른쪽 노드로 들어가 해당 방식을 계속해준다.
중위순회와 비교하기 위해 후위순회의 구현방식도 설명해보자. 후위순회의 print는 왼쪽 재귀와 오른쪽 재귀가 모두 끝난 다음에 위치한다.
즉 오른쪽 노드의 탐색이 끝나야 해당 노드를 출력하게 된다. 이때 중위 노드와 다르게 오른쪽 노드에 진입한다면 해당 부모 노드를 출력하지 않는다.
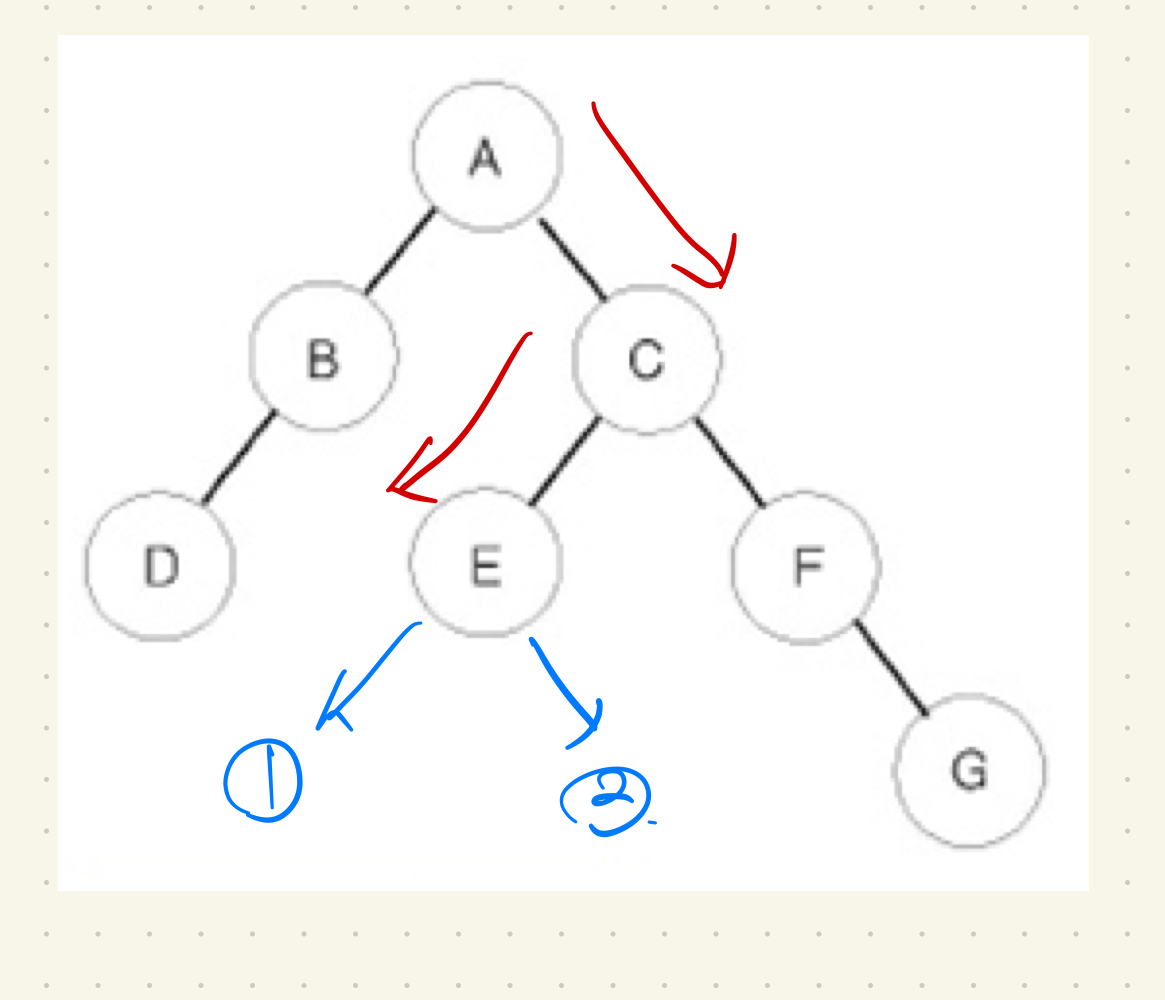
해당 그림에서 중위 순회와 후위 순회의 탐색 순서가 다른 부분은 3번째 부터이다. 여기서부터 살펴보자면
후위 순회의 경우 A에서 왼쪽 탐색이 끝나고, C로 탐색할 수 있다. 즉 C로 진입하게 된다면 A를 출력하지 않는다. 오른쪽 노드의 순회가 끝나지 않았기 때문 (= 오른쪽 노드 이후에 print가 있기 때문에) 이다.
C에서 왼쪽 자식노드 E로 진입한 이후, E의 가상 노드 1 과 2가 모두 없으므로 E를 출력한다.
중위 순회의 경우 전술했던것 처럼 C에 진입하든 말든 상관없이 왼쪽 노드의 탐색이 끝난다면 출력하게 된다.