[기계학습] DNN(Deep Neural Network)을 활용한 축구경기 평점 예측 - 1

게시 2024/09/05

By Yu.S.H 9 분읽는 시간

0. 초안

최근 축구 사이트를 만들어보면서 축구경기와 관련된 많은 데이터를 다루는 기회가 생겼다.

축구에서는 그 선수의 경기 내 활약을 평점 으로 기록하는 점수법이 있는데, 그 평점 시스템을 DNN으로 충분히 만들 수 있을 것 같았다. 흐름은 아래와 같다.

축구선수의 경기 활약은 스텟에 기록된다. ex) 골, 어시스트, 플레잉 시간, 패스성공률 등… (사실)
축구선수의 경기 활약은 평점으로 스코어화 된다. 이때 평점은 평가 기관마다 다를 수 있다. (사실)
1, 2의 관계에서 스탯과 평점은 어느정도 연관이 있다고 가정한다. (가정)
3의 가정에서 스텟(파라미터) 와 평점(라벨)의 데이터를 왕창 구할 수만 있다면, 회귀로 충분히 파라미터에 대한 가중치를 구할 수 있다.

이번 프로젝트에선 예전에 사용해본 Pytorch를 사용해 회귀를 구현해 볼 예정이다. 이번 프로젝트에서 손실함수, 가중치, NN의 작동방식, 역전파 같은 개념들은 자세히 다루지 않기 때문에 만약 개념을 보려면 다른 블로그 글을 추천한다.

1. DNN에 대하여

CNN은 예전에 몇번 다루어 보았지만, 이미지같이 공간적 특성이 있는 데이터와 달리, 더 일반적인 데이터에 대해선 DNN이 효과적이라고 들었다.

CNN과 방법적인 차이는 있지만, 크게 보자면 둘 다 학습에 의해 파라미터의 가중치(Weight)를 조정해, 손실함수(Loss Function)를 최소화하는 것은 동일하다.

1.1 DNN의 정의

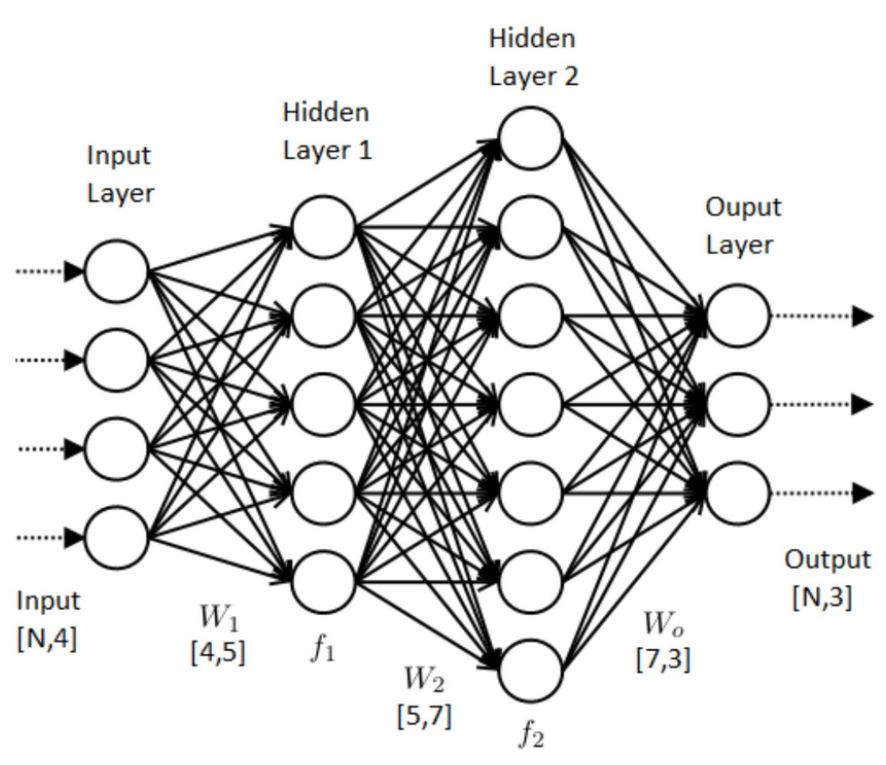
DNN은 여러 은닉층(Hidden Layer)를 완전연결을 통해 연결한 뒤, 들어오는 정보를 통해 파라미터에 대한 가중치를 조정하는 모델이다.

더 일반적인 머신러닝 문제에 효과적이고, 정형화된 그래프, 표형 데이터, 숫자, 시간과 같은 데이터에 적합하다.

1.2 DNN Class

  
class DNNModel(nn.Module):
    def __init__(self):
        super(DNNModel, self).__init__()
        self.layer1 = nn.Linear(입력데이터의 파라미터 수, 128)  # 입력 크기: 특성 개수
        self.layer2 = nn.Linear(128, 64)
        self.layer3 = nn.Linear(64, 32)
        self.output = nn.Linear(32, 1)  # 출력: 평점 (1개의 값)
        self.relu = nn.ReLU()
        
    def forward(self, x):
        x = self.relu(self.layer1(x))
        x = self.relu(self.layer2(x))
        x = self.relu(self.layer3(x))
        x = self.output(x)
        return x

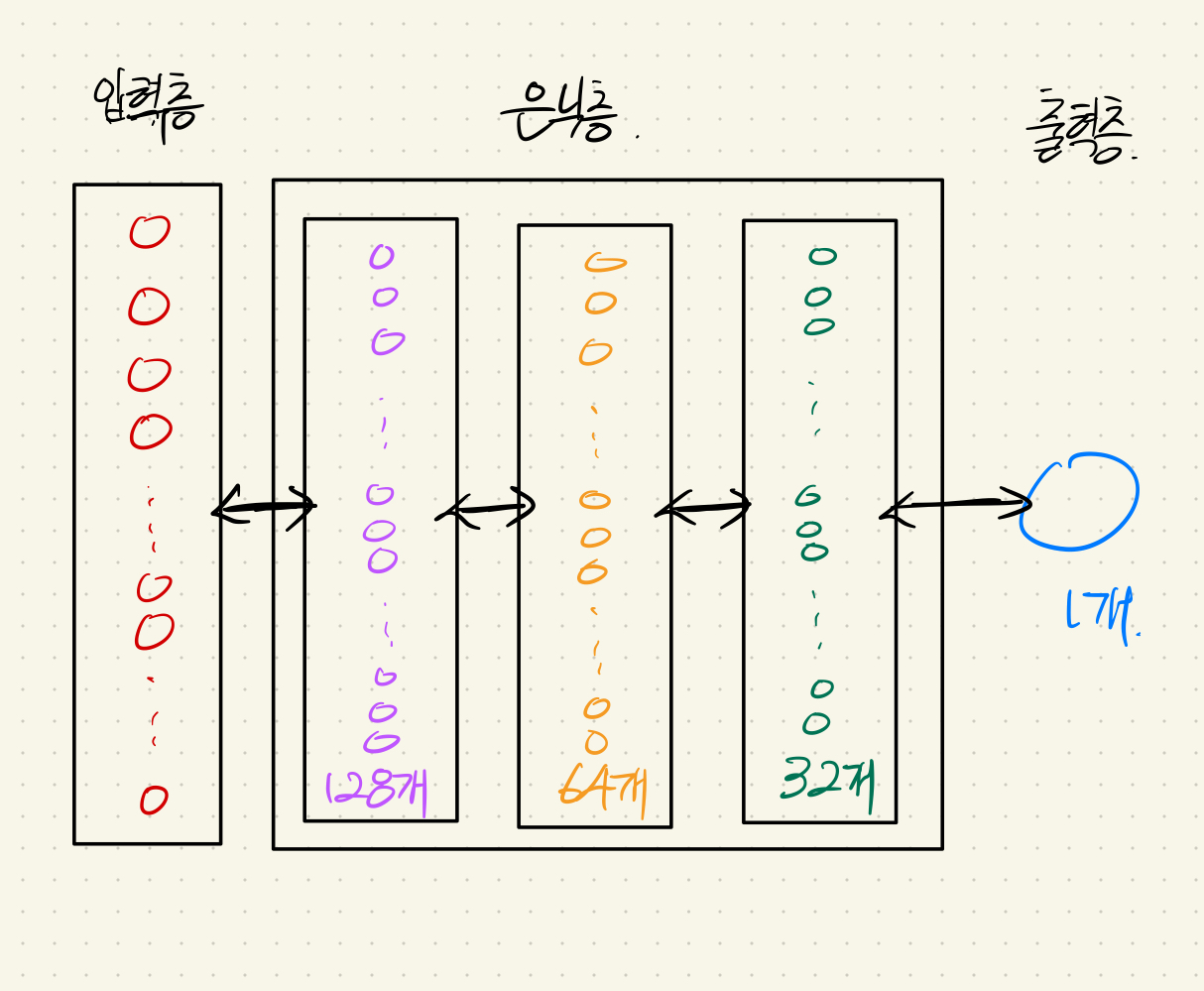
이번에 구성한 모델은 3개의 은닉층(128 → 64 → 32)을 가지게 설정해보았다. (이 값은 무엇이 들어와도 상관 없는 것으로 알고 있다. 대신 층 간의 파라미터 숫자는 맞춰주어야 한다.) 그림으로 표현하면 다음과 같다.

(실제로 모든 파라미터들은 완전히 연결되어 있다. 여기에선 그리기 어려워서 생략…)

너무 많은 층을 구성하는 것은 오히려 가중치 학습에 도움이 안 되는 것으로 안다.(기울기 소실 문제) 따라서 적당한 층을 구성한다.

이때 활성함수는 ReLu를 사용한다. 활성함수에 따라서 가중치의 민감도(역치)를 설정할 수 있다.

2. 과적합(OverFitting) 방지.

단순히 많이 학습시키는 것은 능사가 아니다. 사람이 주입식 교육을 받으면 정해진 문제밖에 해결하지 못하는 것과 같게, 모델에게 너무 많은 학습을 시키는 것은 과적합 문제를 일으킬 수 있다.

즉, 너무 많은 학습은 주어진 학습 세트에선 좋은 성능을 발휘하지만, 새로 추론해야할 데이터에 대해선 좋은 성능을 보여주지 못할 가능성이 생긴다.

과적합 문제를 해결하기 위해 몇 가지 방법을 사용할 계획이다.

2.1 Dropout

Dropout은 학습 과정에서 무작위로 일부 뉴런을 비활성화 시켜, 특정 뉴런에 지나치게 높게 의존하지 않도록 하는 방법이다.

  
class DNNModel(nn.Module):
    def __init__(self):
        super(DNNModel, self).__init__()
        self.layer1 = nn.Linear(입력데이터의 파라미터 수, 128)
        self.layer2 = nn.Linear(128, 64)
        self.layer3 = nn.Linear(64, 32)
        self.output = nn.Linear(32, 1)
        self.relu = nn.ReLU()
        self.dropout = nn.Dropout(p=0.5)  # 50%의 확률로 뉴런 비활성화
        
    def forward(self, x):
        x = self.relu(self.layer1(x))
        x = self.dropout(x)  # 드롭아웃 적용
        x = self.relu(self.layer2(x))
        x = self.dropout(x)  # 드롭아웃 적용
        x = self.relu(self.layer3(x))
        x = self.output(x)
        return x

특정 뉴런의 의존성을 없애 모델이 학습세트에 과도하게 의존하지 않도록 하고, 일반적인 데이터셋 에서도 성능을 보여줄 수 있도록 한다.

2.2 가중치 규제(Weight Regularization)

모델의 가중치가 너무 큰 값을 갖지 않도록 제한한다. 결로 따지면 위 Dropout과 비슷하다.

파이토치에선 optimizer에서 적용할 수 있다.

  
# 옵티마이저에서 가중치 감쇠(weight decay) 사용
optimizer = torch.optim.Adam(model.parameters(), lr=0.001, weight_decay=0.01)

2.3 배치 정규화(Batch Normalization)

각 입력 배치에 대하여 정규화를 진행해 학습을 안정화시킨다.

은닉층 사이에 배치 정규화 층을 삽입해, 출력을 정규화한후, 다음 은닉층으로 전달하는 방식이다.

  
# Batch Normalization 적용
class DNNModel(nn.Module):
    def __init__(self):
        super(DNNModel, self).__init__()
        self.layer1 = nn.Linear(입력데이터의 파라미터 수, 128)
        self.bn1 = nn.BatchNorm1d(128)  # 배치 정규화
        self.layer2 = nn.Linear(128, 64)
        self.bn2 = nn.BatchNorm1d(64)# 배치 정규화
        self.layer3 = nn.Linear(64, 32)
        self.bn3 = nn.BatchNorm1d(32)# 배치 정규화
        self.output = nn.Linear(32, 1)
        self.relu = nn.ReLU()

    def forward(self, x):
        x = self.relu(self.bn1(self.layer1(x)))
        x = self.relu(self.bn2(self.layer2(x)))
        x = self.relu(self.bn3(self.layer3(x)))
        x = self.output(x)
        return x

위 방법들을 적용하면서 하이퍼 파라미터(옵티마이저, 정규화 함수 등)을 조정할 수 있다. epoch에 따라 손실함수의 차이를 그래프로 확인해보자.

Machine Learning

python ai ml dnn football